Matrice nilpotente
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
valsad
- Membre Naturel
- Messages: 73
- Enregistré le: 17 Sep 2009, 08:23
-
 par valsad » 12 Aoû 2010, 11:26
par valsad » 12 Aoû 2010, 11:26
Bonjour,
Soient A et B deux matrices de Mn(R) tel que AB=BA
Je dois montrer que A+B est nilpotente mais je ne sais pas comment m'y prendre.
Pouvez-vous m'aider svp?
Merci.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 12 Aoû 2010, 11:30
par Nightmare » 12 Aoû 2010, 11:30
Salut,
A et B doivent elles même être supposées nilpotentes, sinon c'est évidemment faux (prendre A=B=Id).
Une fois ceci écrit, le fait que nos deux matrices commutent permet, par exemple, d'utiliser la formule du binôme de Newton. Je te laisse exploiter cette piste (c'est quasiment terminé)
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 12 Aoû 2010, 11:31
par girdav » 12 Aoû 2010, 11:31
Bonjour,
je suppose que

et

sont nilpotentes (sinon le résultat est faux : prendre
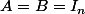
). Essaie le binôme de Newton (licite) à une puissance bien choisie.
édit : il y a même la stéréo!
-
valsad
- Membre Naturel
- Messages: 73
- Enregistré le: 17 Sep 2009, 08:23
-
 par valsad » 12 Aoû 2010, 11:42
par valsad » 12 Aoû 2010, 11:42
j'ai donc supposé qu'il existe k tel que (A+B)^k=0.
J'ai développé (A+B)^k par la formule du binome de newton et j'ai cherché une condition sur k pour que la matrice (A+B)^k=0.
Mon résultat: si A et B sont nilpotentes d'indice a et b alors A+B est nilpotente d'indice k=a+b.
Est-ce la bonne méthode et le bon résultat?
Merci d'avance
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 12 Aoû 2010, 11:51
par girdav » 12 Aoû 2010, 11:51
Ça marche (on montre que
^{a+b} =0)
) mais l'indice de nilpotence de la somme peut ne pas être la somme des indices de nilpotence. Par exemple, tu prends la matrice d'ordre

qui ne contient que des

sauf le terme "en haut à droite" qui est un

. On a que
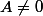
et
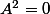
et si on prend
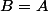
alors
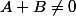
et
^2 = 0)
: l'indice de nilpotence de la somme est 2, tout comme celui de

et celui de

-
valsad
- Membre Naturel
- Messages: 73
- Enregistré le: 17 Sep 2009, 08:23
-
 par valsad » 12 Aoû 2010, 11:57
par valsad » 12 Aoû 2010, 11:57
Mais comme on ne me demande pas l'indice, je peux considérer que si je prends k;)a+b ma matrice A+B sera nilpotente et j'aurai répondu à la question même si je n'ai pas trouvé l'indice, non?
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 12 Aoû 2010, 12:19
par girdav » 12 Aoû 2010, 12:19
Oui, pas la peine de chercher l'indice, il suffit d'établir l'existence d'un rang

pour lequel
^k=0)
.
-
valsad
- Membre Naturel
- Messages: 73
- Enregistré le: 17 Sep 2009, 08:23
-
 par valsad » 12 Aoû 2010, 12:22
par valsad » 12 Aoû 2010, 12:22
Ok Merci!
Dans une autre question, A et B vérifient AB-BA=B et je dois monter que B est nilpotente.
T'aurais un indice pour que faire démarrer?
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 12 Aoû 2010, 12:41
par girdav » 12 Aoû 2010, 12:41
On a
 =0)
pour tout entier

non nul. Ça entraîne que B n'a que des valeurs propres nulles.
-
valsad
- Membre Naturel
- Messages: 73
- Enregistré le: 17 Sep 2009, 08:23
-
 par valsad » 18 Aoû 2010, 09:40
par valsad » 18 Aoû 2010, 09:40
valsad a écrit:Ok Merci!
Dans une autre question, A et B vérifient AB-BA=B et je dois monter que B est nilpotente.
T'aurais un indice pour que faire démarrer?
Bonjour,
Je reviens sur ce sujet:
on a Tr(B^k)=Tr((AB-BA)^k)
Mais Tr((AB-BA)^k)=(Tr(AB-BA))^k?
Merci de votre réponse.
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 18 Aoû 2010, 11:38
par girdav » 18 Aoû 2010, 11:38
C'est vrai ici puisque les deux membres sont nuls mais on n'a pas en général
=(\mathrm{Tr}M)^k)
.
En fait, pour établir que
 = 0)
on écrit que
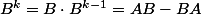B^{k-1} =AB^k-BAB^{k-1})
puis
 = \mathrm{Tr}(AB^{k-1}B) =\mathrm{Tr}(AB^k))
car
=\mathrm{Tr}(NM))
.
-
valsad
- Membre Naturel
- Messages: 73
- Enregistré le: 17 Sep 2009, 08:23
-
 par valsad » 18 Aoû 2010, 11:42
par valsad » 18 Aoû 2010, 11:42
Ok! Merci beaucoup! Je n'avais pas du tout pensé à ça! :we:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 21 invités
^{a+b} =0) ) mais l'indice de nilpotence de la somme peut ne pas être la somme des indices de nilpotence. Par exemple, tu prends la matrice d'ordre
) mais l'indice de nilpotence de la somme peut ne pas être la somme des indices de nilpotence. Par exemple, tu prends la matrice d'ordre  qui ne contient que des
qui ne contient que des  sauf le terme "en haut à droite" qui est un
sauf le terme "en haut à droite" qui est un  . On a que
. On a que 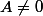 et
et 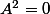 et si on prend
et si on prend 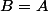 alors
alors 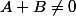 et
et ^2 = 0) : l'indice de nilpotence de la somme est 2, tout comme celui de
: l'indice de nilpotence de la somme est 2, tout comme celui de  et celui de
et celui de 
