j'ai un exercice à résoudre dans lequel on me dit que A est une matrice carrée d'ordre d telle que rg(A)=r
Matrice nilpotente et rang
5 messages
- Page 1 sur 1
Matrice nilpotente et rang
Bonjour, je suis face à un petit problème :
j'ai un exercice à résoudre dans lequel on me dit que A est une matrice carrée d'ordre d telle que rg(A)=r
j'ai un exercice à résoudre dans lequel on me dit que A est une matrice carrée d'ordre d telle que rg(A)=r
D'accord...
Dans ce cas comment pourrais-je aborder la question suivante : montrer qu'il existe deux matrices U (dim dxr) et V (dim rxd) tq rgU=rgV=r et A=UV ?
En fait je pensais trouver une base adaptée au problème (c'est pour ça que j'ai pensé aux matrices nilpotentes), et je ne vois pas vraiment laquelle.
Dans ce cas comment pourrais-je aborder la question suivante : montrer qu'il existe deux matrices U (dim dxr) et V (dim rxd) tq rgU=rgV=r et A=UV ?
En fait je pensais trouver une base adaptée au problème (c'est pour ça que j'ai pensé aux matrices nilpotentes), et je ne vois pas vraiment laquelle.
Bonjour,
Est-ce que tu connais le résultat qui dit qu'une matrice de rang r est équivalente à la matrice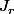 (matrice de dimension dxd, diagonale, avec r 1 puis d - r zéros sur la diagonale) ? Il faut trouver deux bases adaptées (la base d'arrivée est différente de celle de départ) pour que l'application représentée par la matrice s'écrive de cette façon dans ces bases. Dans le cas de J_r les matrices U et V ne sont pas difficiles à trouver.
(matrice de dimension dxd, diagonale, avec r 1 puis d - r zéros sur la diagonale) ? Il faut trouver deux bases adaptées (la base d'arrivée est différente de celle de départ) pour que l'application représentée par la matrice s'écrive de cette façon dans ces bases. Dans le cas de J_r les matrices U et V ne sont pas difficiles à trouver.
choupine a écrit:En fait je pensais trouver une base adaptée au problème (c'est pour ça que j'ai pensé aux matrices nilpotentes), et je ne vois pas vraiment laquelle.
Est-ce que tu connais le résultat qui dit qu'une matrice de rang r est équivalente à la matrice
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 82 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
