
Math spé : polynôme
7 messages
- Page 1 sur 1
Re: Math spé : polynôme
Edit : j'ai dit une connerie à la fin de mon post en disant que le poly partait aux oubliettes dans le développement
là j'en vois pas d'autres mais je bosse dessus
svp ne pas la lire
et une coquille que je viens de corriger mais là rien de grave (comparé à ça)
Bonjour
je ne dis pas que je m'y prend bien mais avez vous essayé de commencer comme ça?
 e^{i\theta } d\theta =)
 \left(cos \theta +i sin\theta \right) d\theta =)
 cos \theta d\theta +i \int _0^{\pi } P\left(e^{i \theta }\right) sin \theta d\theta)
je pose =P\left(e^{i \theta }\right)) et
et 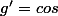 et
et 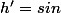
donc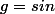 et
et 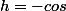
j'essaye de commencer à traiter (enfin si je peux appeler ça traiter vu comme c'est la prise de tête déjà lol)
 cos \theta d\theta = \int _0^{\pi }fg^{\prime }d\theta =\left[fg\right]_0^{\pi }- \int _0^{\pi }f^{\prime } g d\theta)
 sin \theta d\theta = \int _0^{\pi }fh^{\prime }d\theta =\left[fh\right]_0^{\pi }- \int _0^{\pi }f^{\prime } h d\theta)
attention il ne faudra pas oublier i devant cette seconde intégrale quand on fera la somme
en fait l'idée (ça se trouve complètement stupide) c'est de continuer à redévelopper
de la même manière que précédemment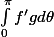 et
et 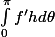
edit connerie(ne pas la lire svp)->>>vu qu'en dérivant successivement on va tomber sur
on va tomber sur 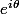 et le polynôme sera parti aux oubliettes dans les deux intégrales et l'intégrale sans le polynôme sera facile à traiter
et le polynôme sera parti aux oubliettes dans les deux intégrales et l'intégrale sans le polynôme sera facile à traiter
(en espérant ne pas avoir dit trop de conneries évidemment)
là j'en vois pas d'autres mais je bosse dessus
svp ne pas la lire
et une coquille que je viens de corriger mais là rien de grave (comparé à ça)
Bonjour
je ne dis pas que je m'y prend bien mais avez vous essayé de commencer comme ça?
je pose
donc
j'essaye de commencer à traiter (enfin si je peux appeler ça traiter vu comme c'est la prise de tête déjà lol)
attention il ne faudra pas oublier i devant cette seconde intégrale quand on fera la somme
en fait l'idée (ça se trouve complètement stupide) c'est de continuer à redévelopper
de la même manière que précédemment
edit connerie(ne pas la lire svp)->>>vu qu'en dérivant successivement
(en espérant ne pas avoir dit trop de conneries évidemment)
Modifié en dernier par azf le 04 Mai 2021, 04:50, modifié 1 fois.
Re: Math spé : polynôme
bon par sécurité j'ai pris un exemple pour voir si ce que j'ai écrit est ok (à part la connerie que j'ai indiqué en édition du message) et c'est ok (d'ailleurs j'ai plein de truc qui s'annulent donc faut pas vous affoler ça à l'air un peu compliqué mais c'est pas mortel)
ceci dit il faut quand même que je développe ce que j'ai fait à partir de ce que j'ai écrit (c'est juste que je voulais voir si j'avais écrit une autre connerie)
ceci dit il faut quand même que je développe ce que j'ai fait à partir de ce que j'ai écrit (c'est juste que je voulais voir si j'avais écrit une autre connerie)
Re: Math spé : polynôme
J'ai été idiot !!!
il fallait éviter d'essayer de faire une IPP (bah oui avec ma dérivée de f je me retrouve avec un truc qui se complique)
bon je vais reprendre à partir de là (ceci dit je ne vous donne pas tout car c'est interdit mais je vais en faire un peu plus quand même)
 e^{i\theta } d\theta =)
 \left(cos \theta +i sin\theta \right) d\theta =)
 cos \theta d\theta +i \int _0^{\pi } P\left(e^{i \theta }\right) sin \theta d\theta)
il fallait éviter d'essayer de faire une IPP (bah oui avec ma dérivée de f je me retrouve avec un truc qui se complique)
bon je vais reprendre à partir de là (ceci dit je ne vous donne pas tout car c'est interdit mais je vais en faire un peu plus quand même)
Re: Math spé : polynôme
cette fois -ci c'est bon : il y a des formules trigonométriques à appliquer du style la formule cos a cos b = ...
 e^{i\theta } d\theta =)
 \left(cos \theta +i sin\theta \right) d\theta =)
 cos \theta d\theta +i \int _0^{\pi } P\left(e^{i \theta }\right) sin \theta d\theta =)


et ça ça s'écrit et ça s'intègre facilement en appliquant la formule trigo sachant que
cos \theta d\theta =)
\right)d\theta +\dfrac {1}{2}\int _a^b cos \left(\theta \left(u-1\right)\right)d\theta)
bon là c'est facile pour démontrer ce qui est demandé (je vous laisse continuer)
et ça ça s'écrit et ça s'intègre facilement en appliquant la formule trigo sachant que
bon là c'est facile pour démontrer ce qui est demandé (je vous laisse continuer)
Re: Math spé : polynôme
Je traiterais un cas simple. Le cas où P est un monome de degré k.
Montrer la propriété en question pour le monome = x^k)
Quand ceci est démontré, on utilise quelques propriétés de base des intégrales pour prouver la propriété proposée.
Montrer la propriété en question pour le monome
Quand ceci est démontré, on utilise quelques propriétés de base des intégrales pour prouver la propriété proposée.
Re: Math spé : polynôme
lyceen95 a écrit:...Quand ceci est démontré, on utilise quelques propriétés de base des intégrales pour prouver la propriété proposée.
bien vu Lycéen95 !
c'est comme ça qu'il faut faire en fait: c'est beaucoup plus simple
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 87 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
