Majoration
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Maelstroo
- Messages: 3
- Enregistré le: 06 Mai 2021, 20:20
-
 par Maelstroo » 06 Mai 2021, 20:28
par Maelstroo » 06 Mai 2021, 20:28
Bonsoir,
Pour montrer la continuité d'une fonction, je cherche à montrer que
^{2}}|)
tend vers 0 lorsque x et y tendent vers 0. Avez-vous des idées de majorations ?
Merci
-
mathelot
 par mathelot » 06 Mai 2021, 20:49
par mathelot » 06 Mai 2021, 20:49
Bonjour,
passe en coordonnées polaires et factorise au maximum
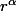
)
)
-
Maelstroo
- Messages: 3
- Enregistré le: 06 Mai 2021, 20:20
-
 par Maelstroo » 06 Mai 2021, 21:09
par Maelstroo » 06 Mai 2021, 21:09
Merci pour la réponse, j'obtiens :
}{r^{8}(cos^{4}+\frac{sin^{2}}{r^{2}})^{2}})
Je ne vois pas trop comment conclure, ne connaissant pas les signes de x,y.
-
mathelot
 par mathelot » 06 Mai 2021, 22:41
par mathelot » 06 Mai 2021, 22:41
bonsoir,
|=\dfrac{r^5(sin^5(\theta)-3r^2cos^4(\theta)\sin^3(\theta))}{r^4(sin^2(\theta)+r^2cos^4(\theta))^2})
il reste à majorer le numérateur et minorer le dénominateur
-
Maelstroo
- Messages: 3
- Enregistré le: 06 Mai 2021, 20:20
-
 par Maelstroo » 07 Mai 2021, 08:04
par Maelstroo » 07 Mai 2021, 08:04
Ok, dernière question :
Est ce qu'on peut dire que
r*(cos/sin) tend vers 0 lorsque r tend vers 0 ?
Si c'est le cas alors c'est bon.
Bonne journée
-
mathelot
 par mathelot » 07 Mai 2021, 17:18
par mathelot » 07 Mai 2021, 17:18
pour
 \neq 0)
,i.e,

différent de 0 , modulo

|=|g(r,\theta)|=|\dfrac{r^5(sin^5(\theta)-3r^2 cos^4(\theta) \sin^3(\theta))}{r^4(\sin^2(\theta)+r^2 \cos^4(\theta))^2}|)
pour
 \neq 0 |f(x,y)| \leq r \, \dfrac{4}{\sin^4(\theta)})
avec
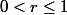
pour
=0 , \, y=0 \, f(x,y)=0)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 26 invités