Majoration d'un polynôme
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 18:30
-
par Nightmare » 29 Nov 2009, 15:24
Salut à tous,
je vous propose de démontrer les résultats suivants :
Soit P un polynôme complexe de degré n (non nul).
1) On suppose que
| < \frac{1}{\sqrt{1-x^2}})
sur [-1,1]. Quelle est alors la meilleure majoration possible pour |P| sur ce segment?
2) On suppose cette fois-ci que
|\leq 1)
toujours sur [-1,1]. Montrer que
| \leq n^{2})
sur [-1,1]
Bon courage
:happy3:
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 18:30
-
par Nightmare » 29 Nov 2009, 18:11
Pas d'idée(s)?
-
Ben314
- Le Ben
- Messages: 21512
- Enregistré le: 11 Nov 2009, 22:53
-
par Ben314 » 29 Nov 2009, 18:22
Ben.... non.
Je pensais à utiliser de l'analyse complexe, sauf que [-1,1], comme contour d'un domaine, c'est pas terrible.
Pour te dire que j'ai un peu cherché, j'ai regardé pour n=1 les contraintes que ca donne (en me disant que c'était un début) mais ca m'a paru une mauvaise idée...
En résumé, j'ai PAS RIEN FAIT m'sieu, mais J'TROUVE PAS !!!
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 18:30
-
par Nightmare » 29 Nov 2009, 18:27
Je n'ai rien trouvé par analyse complexe non plus. La preuve que je connais utilise les polynômes de Tchebytchev si ça peut te mettre sur une piste !
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 12:07
-
par Doraki » 29 Nov 2009, 18:29
| \leq \sqrt{\frac{(n+1)^{n+1}}{n^n}}x^n)
pour
?
-
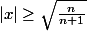
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 18:30
-
par Nightmare » 29 Nov 2009, 18:30
Salut Doraki :happy3:
C'est peut être vrai, mais ce n'est pas la meilleure possible. En fait, la réponse assez surprenante est n-1. Peut être qu'en voyant comment elle est atteinte ça peut vous aider à le montrer.
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 12:07
-
par Doraki » 29 Nov 2009, 18:32
Il faut montrer que par exemple, pour P(x) = 2x, comme |P| satisfait les hypothèses, |P| <= 0 sur [-1;1] ?
Ou ça serait pas plutôt (n+1) ?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 18:30
-
par Nightmare » 29 Nov 2009, 18:33
Oui bien sûr, n+1 :happy3:
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 12:07
-
par Doraki » 29 Nov 2009, 20:20
Si on appelle Pn le polynôme (de degré (n-1)) qui vérifie sin(nx) = Pn(cos(x)) * sin(x),
Pn satisfait la contrainte et en dérivant cette égalité en x=0, on obtient que Pn(1) = n.
Quand tu dis "meilleure majoration possible" ça veut dire quoi précisément ?
Parcequ' on commence avec une majoration par une fonction et tu veux qu'on détermine une majoration uniforme par un réel..
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 18:30
-
par Nightmare » 29 Nov 2009, 20:24
resalut Doraki !
J'ai retranscrit l'énoncé tel que je l'ai eu mais je suis d'accord qu'il n'est pas très clair. Je crois qu'ici il faut concevoir le mot "meilleur" comme "plus simple" :lol3:
Bref, en gros, il s'agit juste de démontrer que P est majoré en module par n+1 comme je l'ai dit.
-
Ben314
- Le Ben
- Messages: 21512
- Enregistré le: 11 Nov 2009, 22:53
-
par Ben314 » 29 Nov 2009, 20:44
Bon, je rapelle que moi, j'ai pas la réponse.....
Mais, par contre (hahaha) j'ai compris l'énoncé (enfin je crois)
On demande le sup de |P(x)| pour tout les polynomes de degrés n (fixé) vérifiant la condition et tout les x dans [-1,1].
j'ai rajouté "fixé" parsqu'au départ, j'avais pas compris et j'était persuadé que le sup était +infini en prenant les "tronquées" du D.V. en série de 1/sqrt(1-x^2)
P.S. c'est quoi le record de longueur d'un post, parce qu'avec le 'e.v.', on pète le plafond... :zen:
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 18:30
-
par Nightmare » 29 Nov 2009, 21:15
Voici l'idée qu'on m'a donnée :
On peut relier notre polynôme P aux polynômes de Tchebytchev
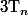
, pour cela, on utilise la base des polynômes de Lagrange.
En notant
,
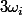
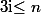
les n racines du polynôme
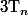
, on a
=\Bigsum_{k=1}^{n} L_{k}(x)P(\omega_{k}))
où les Lk sont les k polynômes d'interpolation de Lagrange associé aux
.
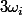
Reste à trouver les L_k en fonction des Tk. Une fois que c'est fait, reste un travail intéressant de majoration que je vous laisse faire :happy3:
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 18:30
-
par Nightmare » 30 Nov 2009, 15:10
Voici la fin du 1) (pour alléger, je suppose mon polynôme de degré n-1 et non n)
On trouve assez facilement que
=\frac{(-1)^{k+1}\sqrt{1-\omega_{k}^{2}}}{n(x-\omega_{k})}T_{n}(x))
Du coup
=\frac{1}{n}\Bigsum_{k=1}^{n} (-1)^{k+1}\sqrt{1-\omega_{k}^{2}}P(\omega_{k})\times \frac{T_{n}(x)}{x-\omega_{k}})
Du coup, l'hypothèse (
|\le 1)
donne :
|\le \frac{1}{n} \Bigsum_{k=1}^{n} \|\frac{T_{n}(x)}{x-\omega_{k}}\|)
Maintenant il reste à distinguer 3 cas :
1) Si
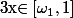
. Les quotients
}{x-\omega_{r}})
sont positifs et du coup
\|\le \frac{1}{n}\Bigsum_{k=1}^{n} \frac{T_{n}(x)}{x-\omega_{r}})
mais le membre de droite n'est autre que
}{n}=\frac{sin(n\theta)}{sin(\theta)})
avec
)
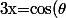Par récurrence on montre que ce machin là est bien majoré par n.
2) Si
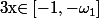
idem
3) Si
,
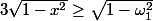
Mais les racines de Tn valent
\pi}{2n})
, d'où ici
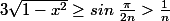
et donc
|\le n)
Dans tous les cas on a bien la majoration par n. C'est le plus petit majorant possible puisque atteint par exemple pour
=\frac{T_{n}'(x)}{n})
(en fait c'est atteint exactement pour les
}{n})
,
)
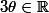
Reste le 2) qui "découle" du 1) sans en être une application directe.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 18:30
-
par Nightmare » 01 Déc 2009, 16:08
Pour ceux que ça intéresse, voici la preuve du 2) :
Le tout est de se ramener au 1.
Posons
=P(cos(\theta)))
. En linéarisant,
)
est de la forme
+\Bigsum_{k=1}^{n} (\lambda_{k}cos(k\theta)+\mu_{k}sin(k\theta)\))
.
L'astuce consiste alors à considérer
=\frac{1}{2}\[Q(\theta+x)-Q(-\theta+x)\])
avec x réel quelconque. Ce choix qui donne un polynôme impair permet d'écrire que
=\Bigsum_{k=1}^{n} \gamma_{k} sin(k\theta))
. Le polynôme
}{sin(\theta)})
pour
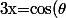vérifie les conditions du 1 et on a donc
}{sin(\theta)}\|\le n)
pour tout
.
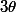
En passant à la limite quand
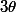
tend vers 0, on obtient
\|\le n)
, c'est à dire
\|\le n)
pour tout x !
Mais
=sin(x)P'(cos(x)))
On obtient alors
P'(cos(x))|\le n)
, ou encore
}\frac{1}{n}P'(cos(x))\|\le 1)
et le 1) appliqué à P'/n donne alors que
)}{n}\|\le n)
et donc
\|\le n^{2})
pour tout theta dans [-1,1].
:happy3:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 33 invités
