Limites par définition
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
lidou
- Messages: 5
- Enregistré le: 07 Oct 2008, 18:00
-
 par lidou » 04 Fév 2009, 11:41
par lidou » 04 Fév 2009, 11:41
bonjour,
je souhaite que vous m'aidez à démontrer "par la définition de la limite" que lim sinx/x=1 lorsque x tend vers zéro
c à d
-1|<\varepsilon)
merci d'avance
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 04 Fév 2009, 12:50
par Joker62 » 04 Fév 2009, 12:50
Généralement pour ce genre de problème
On commence par poser un Epsilon
Et on travaille avec l'inégalité |sin(x)/x - 1| < Epsilon et on cherche à trouver une valeur adéquate pour majorer |x|
-
lidou
- Messages: 5
- Enregistré le: 07 Oct 2008, 18:00
-
 par lidou » 04 Fév 2009, 21:03
par lidou » 04 Fév 2009, 21:03
c'est cette majoration de (valeur absolue de x) que je peine à trouver :mur:
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 04 Fév 2009, 21:05
par XENSECP » 04 Fév 2009, 21:05
euh valeur absolue de x inférieur à 0 ?
-
SimonB
 par SimonB » 04 Fév 2009, 21:05
par SimonB » 04 Fév 2009, 21:05
Ca dépend (fortement) de ta connaissance des fonctions trigonométriques...
Connais-tu les développements limités ?
-
SimonB
 par SimonB » 04 Fév 2009, 21:06
par SimonB » 04 Fév 2009, 21:06
XENSECP a écrit:euh valeur absolue de x inférieur à 0 ?
Je suppose que lidou voulait dire
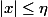
...
-
lidou
- Messages: 5
- Enregistré le: 07 Oct 2008, 18:00
-
 par lidou » 04 Fév 2009, 21:07
par lidou » 04 Fév 2009, 21:07
oui bien sur mais il m'ai demander de trouver une autre méthodes
-
lidou
- Messages: 5
- Enregistré le: 07 Oct 2008, 18:00
-
 par lidou » 04 Fév 2009, 21:11
par lidou » 04 Fév 2009, 21:11
:mur: :mur: :mur:
-
SimonB
 par SimonB » 04 Fév 2009, 21:16
par SimonB » 04 Fév 2009, 21:16
A part utiliser le fait que
}{x} \~ 1)
, je ne vois pas !

-
nuage
- Membre Complexe
- Messages: 2214
- Enregistré le: 09 Fév 2006, 22:39
-
 par nuage » 04 Fév 2009, 21:30
par nuage » 04 Fév 2009, 21:30
Salut,
je ne sais pas comment tu défini la fonction sinus.
Mais, à partir de la définition par le cercle trigonométrique, on a :
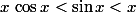
ce qui suffit pour conclure.
[modification]J'ai oublié de préciser pour
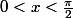
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 44 invités