Ben314 a écrit:Ben ça "saute pas aux yeux" vu que... c'est faux.
Ah bah je pouvais chercher longtemps alors...
Quand je regarde sur internet d'autres cours sur les sous-variétés, la définition par submersion est donnée sous la forme suivante :
Si
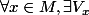
voisinage ouvert de x et
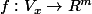
submersion en x tel que
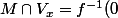)
, alors, M est une sous-variété de dimension n-m.
J'imagine que c'est équivalent à ce qu'on a vu en définissant M directement comme image réciproque d'une valeur régulière (vu que, si j'ai bien compris, être une sous-variété est une propriété locale), mais je ne vois pas trop comment le justifier proprement. Le seul truc que je vois direct, c'est qu'on peut en effet se limiter au cas p=0, quitte à poser g(x)=f(x)-p (les différentielles seront égales, donc le caractère "submersif" sera préservé).
D'autre part, je n'ai pas trouvé de preuve "directe" de cette implication (en utilisant la définition donnée dans le premier post). Cette propriété apparaît souvent dans une "liste" de définitions équivalentes et le sens "(submersion) => (définition)" n'y est jamais prouvé directement...
Du coup j'ai essayé de prouver ça moi-même, voici ce que ça donne :
Par le théorème du rang constant, il existe
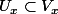
voisinage ouvert de x et
)
difféo tel que
 = (x_1,...,x_m))
Montrons (par double inclusion) que
 = \phi_x(U_x) \cap (R^{n-m} \times \{0_m\}))
1) Soit
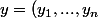 \in \phi_x(U_x \cap M))
 \Leftrightarrow \phi_x^{-1} (y) \in U_x \cap M \Rightarrow f \circ \phi_x^{-1} (y_1,...,y_n) = 0_m)
D'autre part, comme
 \subset \phi_x(U_x))
, on a
=(y_1,...,y_m))
Donc, les m premières coordonnées de y sont nulles et
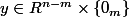
.
Par ailleurs,
 \subset \phi_x(U_x))
Donc,
 \subset \phi_x(U_x) \cap (R^{n-m} \times \{0_m\}))
2) Soit
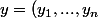 \in \phi_x(U_x) \cap (R^{n-m} \times \{0_m\}))
Il existe
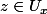
tel que
=y)
On a donc
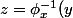 \Rightarrow f(z)=f \circ \phi_x^{-1}(y)=0_m)
car
)
.
Donc,
 \cap U_x=U_x \cap M)
i.e.
)
Donc,
 \supset \phi_x(U_x) \cap (R^{n-m} \times \{0_m\}))
Ca te semble correct ou pas ?
Et, si oui, comment "recoller" ça avec la formulation vue en cours ?
