Limite d'une intégrale à paramètre
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
CC_
- Membre Naturel
- Messages: 69
- Enregistré le: 01 Mai 2006, 13:35
-
 par CC_ » 13 Mar 2008, 22:45
par CC_ » 13 Mar 2008, 22:45
Bonsoir,
J'ai un petit souci pour justifier un résultat sur les intégrales à paramètre. On travaille ici en théorie de Lebesgue et non de Riemann, je précise au cas où !
On pose
 = \int_{\mathbb{R}_+} \, e^{-tx}f(x)\, dx)
, où f est intégrable. Le but est de montrer que
 = 0)
.
On pourrait montrer simplement avec le théorème de convergence dominée, en introduisant la suite d'applications
 = e^{-nx}f(x))
, que
 = 0)
, mais cela ne suffit pas et n'implique pas le résultat que je cherche.
Avez-vous une idée ?
Merci !
-
CC_
- Membre Naturel
- Messages: 69
- Enregistré le: 01 Mai 2006, 13:35
-
 par CC_ » 13 Mar 2008, 23:04
par CC_ » 13 Mar 2008, 23:04
Hello,
Oui mais il me semble qu'il y a un problème. "g(n) tend vers 0" ne me semble pas logiquement équivalent à "g(t) tend vers 0" : on a une suite d'un côté, une fonction de l'autre.
On peut par exemple supposer dans ce type de cas que g(n) = 0 pour tout naturel, mais qu'entre deux naturels, la fonction remonte toujours en y=2, ou ce genre de trucs... Non ?
-
CC_
- Membre Naturel
- Messages: 69
- Enregistré le: 01 Mai 2006, 13:35
-
 par CC_ » 13 Mar 2008, 23:07
par CC_ » 13 Mar 2008, 23:07
Hello,
Oui mais il me semble qu'il y a un problème. "g(n) tend vers 0" ne me semble pas logiquement équivalent à "g(t) tend vers 0" : on a une suite d'un côté, une fonction de l'autre.
On peut par exemple supposer dans ce type de cas que g(n) = 0 pour tout naturel n, mais qu'entre deux naturels, la fonction remonte toujours en y=2, ou ce genre de trucs... Non ?
 par alavacommejetepousse » 13 Mar 2008, 23:10
par alavacommejetepousse » 13 Mar 2008, 23:10
heu
quelle version du théorème de convergence dominée a s tu ?
lf(x,t) l < f(x) avec f intégrable et f(x,t) -> g(x) qd t->t0 en est une naturelle
-
CC_
- Membre Naturel
- Messages: 69
- Enregistré le: 01 Mai 2006, 13:35
-
 par CC_ » 13 Mar 2008, 23:15
par CC_ » 13 Mar 2008, 23:15
Ma version dit :
- si la suite de fonctions
_n)
converge vers

presque partout,
- si

où g est intégrable,
alors

, et donc

.
Dans la tienne,

peut être égal à l'infini sans problème ?
De plus, ta version paraît plus être un mix bizarre entre la convergence dominée et le passage à la limite dans les intégrales...
 par alavacommejetepousse » 13 Mar 2008, 23:17
par alavacommejetepousse » 13 Mar 2008, 23:17
oui
ta version séquentielle permet de montrer "ma version" non séquentielle
pour TOUTE suite tn de limite t0 = +infini
poser
fn(x) = f(tn,x)
-
CC_
- Membre Naturel
- Messages: 69
- Enregistré le: 01 Mai 2006, 13:35
-
 par CC_ » 13 Mar 2008, 23:28
par CC_ » 13 Mar 2008, 23:28
Moui, d'accord, effectivement... Ca ne se devinait pas tout de suite en tout cas ;-)
Merci, bonne soirée et à bientôt !
-
Dyo
- Membre Relatif
- Messages: 124
- Enregistré le: 14 Sep 2007, 10:24
-
 par Dyo » 14 Mar 2008, 07:26
par Dyo » 14 Mar 2008, 07:26
pour TOUTE suite tn de limite t0 = +infini
Je doute sur ça
 = e^{-nx}f(x))
car là tu as choisi une suite
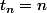
.
Je pense que pour correctement rédiger, il faut considérer au début un suite quelconque
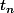
qui tend vers

. Tu poses alors
 = e^{-t_nx}f(x))
et tu peux appliquer la convergence dominée de L.
 par alavacommejetepousse » 14 Mar 2008, 07:44
par alavacommejetepousse » 14 Mar 2008, 07:44
Dyo a écrit:Je doute sur ça
 = e^{-nx}f(x))
car là tu as choisi une suite
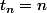
.
Je pense que pour correctement rédiger, il faut considérer au début un suite quelconque
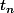
qui tend vers

. Tu poses alors
 = e^{-t_nx}f(x))
et tu peux appliquer la convergence dominée de L.
n'est ce pas exactement ce que j'ai écrit ?
-
Dyo
- Membre Relatif
- Messages: 124
- Enregistré le: 14 Sep 2007, 10:24
-
 par Dyo » 14 Mar 2008, 12:45
par Dyo » 14 Mar 2008, 12:45
n'est ce pas exactement ce que j'ai écrit ?
Exact ^^
Désolé ... je lis un peu trop vite :mur:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 55 invités
