Calcul d'une intégrale à paramètre
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
lefokisetouf
- Membre Naturel
- Messages: 20
- Enregistré le: 17 Juil 2008, 14:50
-
 par lefokisetouf » 12 Jan 2013, 14:17
par lefokisetouf » 12 Jan 2013, 14:17
Bonjour,
Voilà je bloque sur le calcul d'une intégrale à paramètre :
t)}{sin(t)} \, \mathrm dt$)
J'ai essayé beaucoup de choses : IPP, récurrence etc, mais rien n'y fait !
Merci de votre aide !
-
adrien69
- Membre Irrationnel
- Messages: 1899
- Enregistré le: 20 Déc 2012, 12:14
-
 par adrien69 » 12 Jan 2013, 14:33
par adrien69 » 12 Jan 2013, 14:33
Salut,
Tu connais la théorie des séries de Fourier ?
Edit : Désolé Nightmare, j'avais encore quoté.
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 12 Jan 2013, 14:33
par XENSECP » 12 Jan 2013, 14:33
Salut
t\right)} = \sin{(2nt + t)} = \sin{(2nt)}\cos{(t)} + \cos{(2nt)}\sin{(t)})
si ça peut aider un peu

-
Mathusalem
- Membre Irrationnel
- Messages: 1837
- Enregistré le: 14 Sep 2008, 03:41
-
 par Mathusalem » 12 Jan 2013, 14:33
par Mathusalem » 12 Jan 2013, 14:33
lefokisetouf a écrit:Bonjour,
Voilà je bloque sur le calcul d'une intégrale à paramètre :
t)}{sin(t)} \, \mathrm dt$)
J'ai essayé beaucoup de choses : IPP, récurrence etc, mais rien n'y fait !
Merci de votre aide !
Ca fait toujours pi/2.
Essaye avec n=0, n=1. Une fois que tu as confirmé que ça fait pi/2, essaye de le montrer par récurrence.
-
lefokisetouf
- Membre Naturel
- Messages: 20
- Enregistré le: 17 Juil 2008, 14:50
-
 par lefokisetouf » 12 Jan 2013, 15:13
par lefokisetouf » 12 Jan 2013, 15:13
Vaguement, j'ai dû voir ça il y a environ 2 ans...
Y a-t-il moyen de passer oûtre d'après toi ?
Merci de ta réponse si rapide ^^
-
adrien69
- Membre Irrationnel
- Messages: 1899
- Enregistré le: 20 Déc 2012, 12:14
-
 par adrien69 » 12 Jan 2013, 15:24
par adrien69 » 12 Jan 2013, 15:24
Bah le truc c'est que si tu regardes ton intégrande c'est à un changement de variables près le noyau de Dirichlet. Alors ça marche super avec ça.
Edit : Vraiment Nightmare c'est une torture. Pourquoi ils ont appelé ce bouton "répondre" ?!
Editbis : En plus tu n'as pas besoin de connaître la théorie des séries de Fourier pour savoir faire ça, c'est assez automatique, mais c'est plus simple si on sait que ça existe.
-
lefokisetouf
- Membre Naturel
- Messages: 20
- Enregistré le: 17 Juil 2008, 14:50
-
 par lefokisetouf » 12 Jan 2013, 15:32
par lefokisetouf » 12 Jan 2013, 15:32
Tout à fait, il me suffit de poser x=2t ^^
-
adrien69
- Membre Irrationnel
- Messages: 1899
- Enregistré le: 20 Déc 2012, 12:14
-
 par adrien69 » 12 Jan 2013, 16:13
par adrien69 » 12 Jan 2013, 16:13
Voilà voilà ! Et après ça se calcule nickel. Tu me donneras le résultat ? J'ai la flemme de faire le calcul.
Une autre méthode que tu pourrais employer je pense, c'est après avoir fait le changement de variables (si tu ne connais pas Dirichlet), tu développes le sinus. Ça devrait te donner une formule de récurrence.
Edit : Saleté de quotation marks !
-
Mathusalem
- Membre Irrationnel
- Messages: 1837
- Enregistré le: 14 Sep 2008, 03:41
-
 par Mathusalem » 12 Jan 2013, 16:31
par Mathusalem » 12 Jan 2013, 16:31
Pour le résultat, ça donne toujours pi/2.
-
adrien69
- Membre Irrationnel
- Messages: 1899
- Enregistré le: 20 Déc 2012, 12:14
-
 par adrien69 » 12 Jan 2013, 16:34
par adrien69 » 12 Jan 2013, 16:34
Merci pour la réponse Mathusalem.

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 12 Jan 2013, 17:07
par chan79 » 12 Jan 2013, 17:07
lefokisetouf a écrit:Bonjour,
Voilà je bloque sur le calcul d'une intégrale à paramètre :
t)}{sin(t)} \, \mathrm dt$)
J'ai essayé beaucoup de choses : IPP, récurrence etc, mais rien n'y fait !
Merci de votre aide !
Si on pose
t)}{sin(t)} \, \mathrm dt)
on voit vite que

(avec sin p - sin q= ...)
et

-
Mathusalem
- Membre Irrationnel
- Messages: 1837
- Enregistré le: 14 Sep 2008, 03:41
-
 par Mathusalem » 12 Jan 2013, 17:07
par Mathusalem » 12 Jan 2013, 17:07
De manière plus brutale
x)/sin(x) = \frac{e^{i[2n+1]x}-e^{-i[2n+1]x}}{e^{ix}-e^{-ix}})
Or
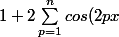 = 1 + \sum \limits_{p=1}^n e^{i2px} + e^{-i2px} = \frac{e^{ix}-e^{-ix}}{e^{ix}-e^{-ix}} +\sum \limits_{p=1}^n \frac{e^{ix}-e^{-ix}}{e^{ix}-e^{-ix}}(e^{i2px} + e^{-i2px}))
x}+e^{i(2p-1)x} - e^{-i(2p-1)x}- e^{-i(2p+1)x}}{e^{ix}-e^{-ix}})
qui est une somme telescopique. Il ne survit plus que le dernier terme
x)/sin(x))
On peut faire le raisonnement à l'envers : essayer de factoriser e^{ix} - e^{-ix} au numérateur de l'expression en sinus, et en fait on se retrouve a construire la somme de cosinus.
Bref, tu peux donc récrire
x)/sin(x) = \int \limits_{0}^{\pi/2} 1 + 2\sum \limits_{p=1}^{n}cos(2nx))
La primitive est alors triviale. Tu peux remarquer quand même que les fonctions cosinus sont anti-symétriques sur l'intervalle d'intégration et ne contribuent donc pas. Donc, l'intégrale donnera

Edit ; je préfère la méthode de Chan79
-
lefokisetouf
- Membre Naturel
- Messages: 20
- Enregistré le: 17 Juil 2008, 14:50
-
 par lefokisetouf » 13 Jan 2013, 12:22
par lefokisetouf » 13 Jan 2013, 12:22
Avec la première méthode, je trouve effectivement pi/2 très facilement !
Merci à tous ^^
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 44 invités
t)}{sin(t)} \, \mathrm dt$)