Limite d'une intégrale à paramètre

[Wenneguen]

Bonjour,

j'aimerais calculer la limite en 0 de .
Je pense donc à un théorème de convergence dominée pour intervertir limite et intégrale, mais celui-ci s'utilise en principe dans le cas d'une limite de la forme , ce qui n'est pas le cas ici.
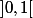
Puis-je cependant m'y ramener en déclarant que , avec une suite quelconque d'éléments de (le domaine de définition de f) telle que ?

Merci.

[barbu23]

Bonsoir, :happy3:
Il me semble qu'il faut utiliser là, le théorème de continuité en concernant les intégrales à paramètres, c'est à dire, établir que : , et donc est la valeur de cette limite qu'il faut essayer de calculer je pense.
J'attends la confirmation des autres.
Cordialement.

[adrien69]

Tu peux bien t'y ramener en considérant toutes les suites tendant vers 0 (par valeurs positives ici je suppose), mais ce n'est pas le théorème de convergence dominée que tu vas devoir utiliser mais celui de convergence monotone, qui s'applique à des fonctions positives qui ne sont pas intégrables.