Les polynomes

[aissayoub]

quelqu'un a une idée comment on démontre la première question à l'aide de la récurrence

[mathelot]

Bonjour,
lire ici
https://fr.wikipedia.org/wiki/Polyn%C3% ... Tchebychev
comment la formule de Simpson avec les cosinus,donne une formule de récurrence
sur les polynômes

[aissayoub]

mais dans l'exercice on a pas cette hypothèse

[mathelot]

je pense qu'il est possible d'utiliser cette formule de récurrence après l'avoir démontrée d'après les formules de Simpson
cos(a+b) + cos(a-b)=2 cos(a) cos(b)

[Tuvasbien]

Bonjour, l'unicité est facile à montrer (seul le polynôme nul admet une infinité de racines). Avec les formules de trigonométrie, développe et puis utilise l'unicité pour aboutir à 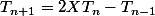. D'ailleurs je ne sais pas si le raisonnement par récurrence est imposé ou non mais tu peux t'en passer et éviter de démontrer cette formule de récurrence.

[mathelot]

sinon, il y a une autre méthode à partir de la formule de De moivre:



qui donne un polynôme de la quantité cos(x). Mais bon, ça utilise le développement du binôme.

[aissayoub]

Merci beaucoup , c'est bon j'ai trouvé