Les ouverts de IN^IN muni de la topologie produit.
25 messages
- Page 1 sur 2 - 1, 2
Les ouverts de IN^IN muni de la topologie produit.
Bonjour à tous,
si l'on muni IN de la topologie discrète, c'est-à-dire que toutes les parties de IN sont des ouverts. Et que l'on muni ensuite IN^IN de la topologie produit.
Est-ce que toutes les parties de IN^IN sont des ouverts ?
Je me demande si je ne confonds pas la topologie boite avec la topologie produit...
si l'on muni IN de la topologie discrète, c'est-à-dire que toutes les parties de IN sont des ouverts. Et que l'on muni ensuite IN^IN de la topologie produit.
Est-ce que toutes les parties de IN^IN sont des ouverts ?
Je me demande si je ne confonds pas la topologie boite avec la topologie produit...
Oui elles coïncident pour un nombre fini d'espaces (enfin je pense, je ne me suis pas assuré de le chose, mais c'est probable).
La topo produit est celle engendrée par la base de topologie des ouverts élémentaires.
Les ouverts élémentaires sont les intersections finies d'inverses de projections d'ouverts de X. On projette IN^IN sur chacun des IN. On veut que les projections soient continues afin de pouvoir utiliser la propriété universelle.
Dans notre exemple, X=IN.
J'espère être assez clair, c'est pas facile à écrire lorsqu'on ne maitrise pas LATEX.
J'ai un peu de mal à visualiser les ouverts de IN^IN pour cette topologie.
La topo produit est celle engendrée par la base de topologie des ouverts élémentaires.
Les ouverts élémentaires sont les intersections finies d'inverses de projections d'ouverts de X. On projette IN^IN sur chacun des IN. On veut que les projections soient continues afin de pouvoir utiliser la propriété universelle.
Dans notre exemple, X=IN.
J'espère être assez clair, c'est pas facile à écrire lorsqu'on ne maitrise pas LATEX.
J'ai un peu de mal à visualiser les ouverts de IN^IN pour cette topologie.
Je suis bien d'accord avec ton argument... Mais que montres-tu avec cela ? Je ne vois ce que tu essaies de montrer avec cela.
En fait je voulais utiliser le même argument pour montrer qu'une application de IN^IN dans les irrationnels était continue mais comme toutes les parties de IN^IN ne sont pas des ouverts, ça ne marche pas. :triste:
En fait je voulais utiliser le même argument pour montrer qu'une application de IN^IN dans les irrationnels était continue mais comme toutes les parties de IN^IN ne sont pas des ouverts, ça ne marche pas. :triste:
Zapata a écrit:Je suis bien d'accord avec ton argument... Mais que montres-tu avec cela ? Je ne vois ce que tu essaies de montrer avec cela.
En fait je voulais utiliser le même argument pour montrer qu'une application de IN^IN dans les irrationnels était continue mais comme toutes les parties de IN^IN ne sont pas des ouverts, ça ne marche pas. :triste:
tu as raison, je ne sais pas pourquoi je me suis dit que les projections vont de IN dans IN^IN alors que c'est le contraire.
Zapata a écrit:Je suis bien d'accord avec ton argument... Mais que montres-tu avec cela ? Je ne vois ce que tu essaies de montrer avec cela.
En fait je voulais utiliser le même argument pour montrer qu'une application de IN^IN dans les irrationnels était continue mais comme toutes les parties de IN^IN ne sont pas des ouverts, ça ne marche pas. :triste:
tu as raison, je ne sais pas pourquoi je me suis dit que les projections vont de IN dans IN^IN alors que c'est le contraire. :marteau:
attends je récapitule: y a deux questions en fait:
On prend IN^IN muni de la topo produit.
1) Montrer que les projections sont continues.
2) montrer qu'une application de IN^IN dans les irrationnels est continue.
(c'est quoi la "propriété universelle"?)
La topo produit est celle engendrée par la base de topologie des ouverts élémentaires.
Les ouverts élémentaires sont les intersections finies d'inverses de projections d'ouverts de X
On prend IN^IN muni de la topo produit.
1) Montrer que les projections sont continues.
2) montrer qu'une application de IN^IN dans les irrationnels est continue.
(c'est quoi la "propriété universelle"?)
La topo produit est celle engendrée par la base de topologie des ouverts élémentaires.
Les ouverts élémentaires sont les intersections finies d'inverses de projections d'ouverts de X
Bonjour,
Définition de la topologie produit (version langage mathématique de celle que Zapata a donnée plus haut):
Soient_{i \in I}) une famille d'espaces topologiques.
une famille d'espaces topologiques.
Les rectangles ouverts sur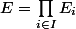 sont (c'est une définition) les ensembles de la forme
sont (c'est une définition) les ensembles de la forme 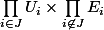 , où J est un sous-ensemble fini de I et les
, où J est un sous-ensemble fini de I et les 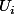 sont des ouverts de
sont des ouverts de 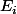 .
.
On définit les ouverts de E comme les réunions (finies ou infinies) de rectangles ouverts.
On montre que c'est bien une topologie, et que c'est la topologie la moins fine qui rende continue les projections sur les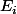 .
.
Dans le cas qui nous intéresse,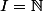 et pour tout i,
et pour tout i, 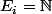 muni de la topologie discrète, donc un rectangle ouvert de
muni de la topologie discrète, donc un rectangle ouvert de 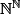 a un nombre fini de composantes qui sont des parties quelconques de
a un nombre fini de composantes qui sont des parties quelconques de  , et les autres qui sont égales à
, et les autres qui sont égales à  , et les réunions de tels rectangles sont aussi de cette forme.
, et les réunions de tels rectangles sont aussi de cette forme.
Définition de la topologie produit (version langage mathématique de celle que Zapata a donnée plus haut):
Soient
Les rectangles ouverts sur
On définit les ouverts de E comme les réunions (finies ou infinies) de rectangles ouverts.
On montre que c'est bien une topologie, et que c'est la topologie la moins fine qui rende continue les projections sur les
Dans le cas qui nous intéresse,
J'édite mon message suite à la réponse de ABC, ceci était pour legéniedesalpages :
Tu as tout à fait raison, mais en fait si tu veux on définit la topologie produit afin que les projections soient continues, c'est un axiome, donc inutile de le démontrer. Ce que tu as fait est donc évidemment juste et tu exprimes bien ce que je veux dire par ouverts élémentaires.
Ce que j'entends par prop universelle, c'est que si tu as
f une appli de T dans X x Y, et que pr : X x Y dans X (projection sur X) et pr : X x Y dans Y (les projections sont donc continues) et que les deux pr°f (pr "rond" f) sont continues, alors f est continue.
Cela est valable aussi dans le cadre d'un produit quelconque d'espaces, en particulier IN^IN.
Le but de ma question est en fait de montrer que II est homéomorphe à IN^IN muni de la topologie produit (beau résultat, sachant que II n'est pas dénombrable...).
Après avoir construit une appli f bien particulière, je voudrai montrer qu'elle et son inverse (qui existe car j'ai montré que c'etait une bijection) sont continues. Je voulais utiliser le fait que IN^IN est discret pour la topologie produit mais ça ne marche pas, (puisque les parties de IN^IN ne sont pas ouvertes pour cette topologie). Donc je cherche une autre méthode.
Pour cela, je voulais simplement avoir un peu d'aide pour "décrire" les ouverts de IN^IN, car je voudrai montrer que si j'ai une boule ouverte dans II, alors son image inverse est un ouvert dans IN^IN, afin de montrer la continuité de f...
Ouf ! J'y arrive !
Mais je n'ai hélas pas le temps de détailler plus mon travail, ni le fameux "f" en question. Si ça t'intéresse (car c'est très intéressant), je pourrai toujours scanner le travail et son énoncé... Mais pas pour le moment, je n'ai pas le matériel adéquat.
Merci en tout cas pour ton aide, je ne m'exprime pas toujours très clairement !
Oui, tu as tout a fait raison ABC, les ouverts sont bien de cette forme là !
Tu as tout à fait raison, mais en fait si tu veux on définit la topologie produit afin que les projections soient continues, c'est un axiome, donc inutile de le démontrer. Ce que tu as fait est donc évidemment juste et tu exprimes bien ce que je veux dire par ouverts élémentaires.
Ce que j'entends par prop universelle, c'est que si tu as
f une appli de T dans X x Y, et que pr : X x Y dans X (projection sur X) et pr : X x Y dans Y (les projections sont donc continues) et que les deux pr°f (pr "rond" f) sont continues, alors f est continue.
Cela est valable aussi dans le cadre d'un produit quelconque d'espaces, en particulier IN^IN.
Le but de ma question est en fait de montrer que II est homéomorphe à IN^IN muni de la topologie produit (beau résultat, sachant que II n'est pas dénombrable...).
Après avoir construit une appli f bien particulière, je voudrai montrer qu'elle et son inverse (qui existe car j'ai montré que c'etait une bijection) sont continues. Je voulais utiliser le fait que IN^IN est discret pour la topologie produit mais ça ne marche pas, (puisque les parties de IN^IN ne sont pas ouvertes pour cette topologie). Donc je cherche une autre méthode.
Pour cela, je voulais simplement avoir un peu d'aide pour "décrire" les ouverts de IN^IN, car je voudrai montrer que si j'ai une boule ouverte dans II, alors son image inverse est un ouvert dans IN^IN, afin de montrer la continuité de f...
Ouf ! J'y arrive !
Mais je n'ai hélas pas le temps de détailler plus mon travail, ni le fameux "f" en question. Si ça t'intéresse (car c'est très intéressant), je pourrai toujours scanner le travail et son énoncé... Mais pas pour le moment, je n'ai pas le matériel adéquat.
Merci en tout cas pour ton aide, je ne m'exprime pas toujours très clairement !
Oui, tu as tout a fait raison ABC, les ouverts sont bien de cette forme là !
désolé j'ai cru que c'était ce que tu voulais montrer, surtout que dans mon cours ce n'est pas un axiome mais une propriété immédiate, je n'ai étudié que les produits finis d'espaces et la topologie dessus est défini avec des ouverts élémentaires d'une façon similair aux rectangles de abcd22.
Par II tu sous-entends l'ensemble des irrationnels?
Par II tu sous-entends l'ensemble des irrationnels?
Pas de soucis ! j'étais pas très clair non plus.
Oui II c'est bien les irrationnels, c'est un I avec une double barre mais II ne rend pas très bien...
Et donc c'est bien dans le cadre infini qu'il y a une différence entre la topologie boite et topologie produit...
Dans la définition de abcd22, pour la topo boite, le J peut-être infini. Alors que pour la topo produit non.
La topologie c'est trop fort !
:++:
Oui II c'est bien les irrationnels, c'est un I avec une double barre mais II ne rend pas très bien...
Et donc c'est bien dans le cadre infini qu'il y a une différence entre la topologie boite et topologie produit...
Dans la définition de abcd22, pour la topo boite, le J peut-être infini. Alors que pour la topo produit non.
La topologie c'est trop fort !
:++:
Héhé !
C'est pas facile en effet, mais avec un fil directeur ça va, en fait en gros on construit une famille d'intervalles de plus en plus petits indicée par (a,z,e,r,t,y,u,i,...) avec a,z,e,r,t,y,u,i,... qui appartiennent à IN (on voit se profiler IN^IN) et on montre qu'à "l'infini", il n'y a qu'un seul irrationnel dans chaque intervalle, et que chaque intervalle contient un irrationnel... Voilà !
Je pourrais te filer l'énoncé si tu veux. Ça vaut la peine de méditer un peu.
C'est pas facile en effet, mais avec un fil directeur ça va, en fait en gros on construit une famille d'intervalles de plus en plus petits indicée par (a,z,e,r,t,y,u,i,...) avec a,z,e,r,t,y,u,i,... qui appartiennent à IN (on voit se profiler IN^IN) et on montre qu'à "l'infini", il n'y a qu'un seul irrationnel dans chaque intervalle, et que chaque intervalle contient un irrationnel... Voilà !
Je pourrais te filer l'énoncé si tu veux. Ça vaut la peine de méditer un peu.
Zapata a écrit:Héhé !
C'est pas facile en effet, mais avec un fil directeur ça va, en fait en gros on construit une famille d'intervalles de plus en plus petits indicée par (a,z,e,r,t,y,u,i,...) avec a,z,e,r,t,y,u,i,... qui appartiennent à IN (on voit se profiler IN^IN) et on montre qu'à "l'infini", il n'y a qu'un seul irrationnel dans chaque intervalle, et que chaque intervalle contient un irrationnel... Voilà !
Je pourrais te filer l'énoncé si tu veux. Ça vaut la peine de méditer un peu.
lol, une famille d'intervalles indexée par un clavier.
Oui quand t'as un peu de temps je veux bien que tu me passes l'énoncé, ça m'intéresse.
25 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 26 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
