Salut Aviateur,
Si tu veux bien qu'on revienne sur cette intégrale.. !
Voici une autre méthode qui m'a aussi beaucoup plu. Tous les passages à justifier (a posteriori) seront notés par un (*)
Introduisons l'intégrale paramétrique:
 = \int_{0}^{1} \frac{x^j}{(x^2 + ax + b)^{m+1}}ln(ln(\frac{1}{x}))dx)
en supposant que le dénominateur possède deux racines complexes conjuguées (discriminant négatif strict).
On met donc
)
sous forme polaire
)
avec donc:
 = \int_{0}^{1} \frac{x^j}{(x^2 - 2rxcos(\theta) + r^2)^{m+1}}ln(ln(\frac{1}{x}))dx)
Première étape: évaluons
 = \int_{0}^{1} \frac{ln(ln(\frac{1}{x}))}{(x^2 - 2xcos(\theta) + 1)}dx) ((*) Lemme à prouver par la suite)
((*) Lemme à prouver par la suite): Utilisons le lemme d'interversion des sommations suivant:
Si P est de la forme d'un DSE,
 = \sum_{n=0}^{\infty}a_nx^n)
, nous avons:
 ln(ln(\frac{1}{x})) = - \gamma L_{P}(1) + L'_{P}(1))
avec L qui désigne
 = \sum_{n=0}^{\infty} \frac{a_n}{(n+1)^s})
Maintenant, pour tout
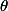
n'annulant pas
)
, nous avons
 = \frac{1}{sin(\theta)} \int_{0}^{1} \frac{sin(\theta) ln(ln(\frac{1}{x}))}{(x^2 - 2xcos(\theta) + 1)}dx)
qui incite à poser
 = \frac{sin(\theta)}{(x^2 - 2xcos(\theta) + 1)})
qui n'a pas de singularités polaires par hypothèse. P(x) a un DSE de la forme:
 = \sum_{k=0}^{k=\infty} sin((k+1)\theta))x^k)
(**)
Cela permet d'extraire
 = \sum_{k=0}^{\infty} \frac{sin((k+1)\theta)}{(k+1)^s})
Maintenant nous essayons d'appliquer le Lemme d'interversion il nous faut donc les valeurs de L(1) et L'(1).
Pour
 = L_{P}(1) = \frac{\pi - \theta}{2})
par le théorème de Dirichlet (en utilisant la transformée de Fourier d'une fonction C1 par morceaux, en tout point de continuité).
La dérivée de L vaut
(**) = \frac{-\pi}{2}((\gamma + ln(2 \pi))( \frac{\theta}{\pi} - 1) + ln(\frac{\Gamma(\theta/2\pi) }{\Gamma(1 - \theta/2\pi)}))
.
On établit
(***) ensuite que:
}(r ; \theta) = \frac{-1}{2 r sin(\theta)} \frac{\partial G_{0,0}(r ; \theta)}{\partial{ \theta}})
Soit plus explicitement, en faisant intervenir la fonction Digamma (
)
):
(E)}(1 ; \theta) = \frac{ln(2 \pi)}{4 sin^2(\theta)} (1 + (\pi - \theta) cot(\theta)) + \frac{1}{sin^2{\theta}}(\Psi(\theta/2\pi) + \Psi(1 - \theta/2\pi)) + \frac{\pi}{4} csc^2(\theta) cot(\theta) ln(\frac{\Gamma(1 - \theta/2\pi)}{\Gamma(\theta/2\pi)})})
Finalement, la question posée du calcul de
 }{cosh^{n+1}(t)})
se ramène par changement de variable
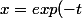)
au calcul de
)}{(x^2 + 1)^{n+1}} dx)
qui n'est autre que
)
.
En remplaçant dans (E) par les valeurs souhaitées et en utilisant des valeurs remarquables de la fonction Digamma, comme Digamma(1/4) et Digamma(3/4), nous aboutissons à:
}{ch^2(x)}dx = -\gamma + ln(\frac{\pi}{4}))
et à un moyen de calculer l'intégrale pour plusieurs exposants possibles.