Inéquation variationnelle
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
sarah2
- Messages: 3
- Enregistré le: 21 Avr 2017, 20:36
-
par sarah2 » 21 Avr 2017, 22:20
Bonsoir
J'ai besoin de votre aide svp.
je veux trouver La formulation variationnelle de problème suivant
Nous recherchons une fonction
tq:
u-f \leq 0~,~~~~~~(1)~~~~u-\psi \leq 0~~~\\ \\ \mathbf{(- \dfrac{\partial u}{\partial t}+\mathbf{A}(t)u-f)(u-\psi)=0~~in~~\mathsf{Q}} ~~~~~~~~~~(\mathsf{Q}= \Omega \times ]0,T[)\\)
=\bar{u}(x),~~x\in \Omega,})
l'opérateur
est donné par:
u= -\sum \dfrac{\partial}{\partial x_i}(a_{ij}(x,t)\dfrac{\partial u}{\partial x_j})+\sum a_j(x,t) \dfrac{\partial u}{\partial x_j}+a_o(x,t)u.})
tq:
,~a_j(x,t),~a_o(x,t) \in \mathsf{L}^\infty(\mathsf{Q})~~and~~f, \psi \in \mathsf{L}^2(0,T;H).})
j'ai multiplié l'inéquation (1) par une fonction test
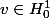
et j'ai intégré sur
(j'ai utilisé formule de green)
mon problème est est-ce-que l'inéquation (1) rester
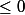
ou nn ?????
Merci en avance.
-
aviateur
par aviateur » 22 Avr 2017, 08:12
Bonjour, Il s'agit d'une inéquation variationnelle qu'il faut trouver. On ne procède donc pas comme une équation variationnelle.
C'est à dire que si
il faut multiplier (1) par (v-u) où
.
-
sarah2
- Messages: 3
- Enregistré le: 21 Avr 2017, 20:36
-
par sarah2 » 22 Avr 2017, 19:14
salut
et oui bien sûr en va choisir
tq :
)
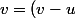mon problème est : est-ce-que
u-f) v dx \leq 0~~~~~~~~~1)
ou bien
u-f) v dx \geq 0~~~~~~~~2)
puisque si
alors on obtient 2 mais si
on obtient 1
merci
-
aviateur
par aviateur » 22 Avr 2017, 19:55
Bonjour,
Je ne suis pas d'accord on multiplie par v-u (et non pas par v=v-u).
Ensuite il faut voir que v-u=(v-\psi) -(u-\psi). Ensuite dans les intégrales les termes qui interviennent sont ou bien nuls ou bien ont un signe connus. Je n'ai rien écrit mais cela devrait marcher
-
sarah2
- Messages: 3
- Enregistré le: 21 Avr 2017, 20:36
-
par sarah2 » 22 Avr 2017, 20:03
merci pour votre réponse
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 34 invités
