Valeur absolue et inéquation
38 messages
- Page 1 sur 2 - 1, 2
Valeur absolue et inéquation
Bonsoir, j'ai du mal dans les résolutions avec les valeurs absolues et j'aimerais avoir une correction pour cet exercice :
On me demande de résoudre |x²+x-4|>= 2x-1.
Ce que j'ai fait :
1) Etude de x²+x-4: x²+x-4>0 sur ]-oo; (-1-rac17)/2[U](-1+rac17)/2;+oo[ et x²+x-4<0 sur ](-1-rac17)/2;(-1+rac17)/2[.
2) Pour x appartient à ]-oo; (-1-rac17)/2[U](-1+rac17)/2;+oo[ alors |x²+x-4|>= 2x-1 est équivalent à x²+x-4>=2x-1. Soit x²-x-3>=0. Les solutions sont donc ici : S1=]-oo;(1-rac13)/2[U](1+rac13)/2;+oo[.
3) Pour x appartient à ](-1-rac17)/2;(-1+rac17)/2[, |x²+x-4|>= 2x-1 équivaut à -x²-x+4>= 2x-1 soit -x²-3x+5>=0 donc S2=](-3-rac29)/2;-3+rac29/2[.
Donc solutions : S=](1-rac13)/2;-3+rac29/2[.
merci de corriger.
On me demande de résoudre |x²+x-4|>= 2x-1.
Ce que j'ai fait :
1) Etude de x²+x-4: x²+x-4>0 sur ]-oo; (-1-rac17)/2[U](-1+rac17)/2;+oo[ et x²+x-4<0 sur ](-1-rac17)/2;(-1+rac17)/2[.
2) Pour x appartient à ]-oo; (-1-rac17)/2[U](-1+rac17)/2;+oo[ alors |x²+x-4|>= 2x-1 est équivalent à x²+x-4>=2x-1. Soit x²-x-3>=0. Les solutions sont donc ici : S1=]-oo;(1-rac13)/2[U](1+rac13)/2;+oo[.
3) Pour x appartient à ](-1-rac17)/2;(-1+rac17)/2[, |x²+x-4|>= 2x-1 équivaut à -x²-x+4>= 2x-1 soit -x²-3x+5>=0 donc S2=](-3-rac29)/2;-3+rac29/2[.
Donc solutions : S=](1-rac13)/2;-3+rac29/2[.
merci de corriger.
pluie2 a écrit:Bonsoir, j'ai du mal dans les résolutions avec les valeurs absolues et j'aimerais avoir une correction pour cet exercice :
On me demande de résoudre |x²+x-4|>= 2x-1.
Ce que j'ai fait :
1) Etude de x²+x-4: x²+x-4>0 sur ]-oo; (-1-rac17)/2[U](-1+rac17)/2;+oo[ et x²+x-4= 2x-1 est équivalent à x²+x-4>=2x-1. Soit x²-x-3>=0. Les solutions sont donc ici : S1=]-oo;(1-rac13)/2[U](1+rac13)/2;+oo[.
3) Pour x appartient à ](-1-rac17)/2;(-1+rac17)/2[, |x²+x-4|>= 2x-1 équivaut à -x²-x+4>= 2x-1 soit -x²-3x+5>=0 donc S2=](-3-rac29)/2;-3+rac29/2[.
Donc solutions : S=](1-rac13)/2;-3+rac29/2[.
merci de corriger.
salut
si 2x-1 est négatif ou nul soit
Donc tous les nombres inférieurs ou égaux à 1/2 sont des solutions.
Ensuite, il faut voir pour les valeurs supérieures à 1/2
chan79 a écrit:salut
si 2x-1 est négatif ou nul soitalors l'inégalité est vérifiée
Donc tous les nombres inférieurs ou égaux à 1/2 sont des solutions.
Ensuite, il faut voir pour les valeurs supérieures à 1/2
en fait je ne comprends pas pourquoi il faut à chaque fois traiter les deux cas et surtout pourquoi ma méthode ne marche pas (dedans, je ne prends pas en compte le 1/2 je résous juste pour inférieur ou égal à 0...).
De plus, dans mon cours, j'ai cette formule :
|a|=0) donc ici ça ferait : |a|>=b si (-b>=a>=b et b<=0) ?
[quote="pluie2"]en fait je ne comprends pas pourquoi il faut à chaque fois traiter les deux cas et surtout pourquoi ma méthode ne marche pas (dedans, je ne prends pas en compte le 1/2 je résous juste pour inférieur ou égal à 0...).
De plus, dans mon cours, j'ai cette formule :
|a|=0) donc ici ça ferait : |a|>=b si (-b>=a>=b et b0 on élève au carré et on a
(x²+3x-5)(x²-x-3)>=0
finalement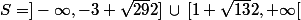
De plus, dans mon cours, j'ai cette formule :
|a|=0) donc ici ça ferait : |a|>=b si (-b>=a>=b et b0 on élève au carré et on a
(x²+3x-5)(x²-x-3)>=0
finalement
[quote="pluie2"]en fait je ne comprends pas pourquoi il faut à chaque fois traiter les deux cas et surtout pourquoi ma méthode ne marche pas (dedans, je ne prends pas en compte le 1/2 je résous juste pour inférieur ou égal à 0...).
De plus, dans mon cours, j'ai cette formule :
|a|=0) donc ici ça ferait : |a|>=b si (-b>=a>=b et b=b si (-b>=a>=b et b=b est toujours vraie quelque soit a.
Revenons à ton exercice. Ta méthode est correcte, mais elle n'aboutit pas car tu as fait des erreurs dans la résolution.
Voici la méthode que tu as utilisée:
Tu as partitionné R en 2 parties P1 et P2 et c'est ce que tu as développé dans 1), jusque là tout est bon.
Ensuite dans 2) tu as résolu l'inéquation pour x appartenant à P1 et tu as trouvé l'ensemble S1 comme solutions. Mais tu as oublié que tu as résolu l'inéquation dans P1 et non pas dans R. L'ensemble des solutions est donc S'1 = P1 inter S1.
Même remarque pour la 3), l'ensemble des solutions est S'2 = P2 inter S2.
Et l'ensemble des solutions de l'inéquation dans R est égal à l'ensemble des solutions dans P1, union, l'ensemble des solutions dans P2, soit S = S'1 U S'2
De plus, dans mon cours, j'ai cette formule :
|a|=0) donc ici ça ferait : |a|>=b si (-b>=a>=b et b=b si (-b>=a>=b et b=b est toujours vraie quelque soit a.
Revenons à ton exercice. Ta méthode est correcte, mais elle n'aboutit pas car tu as fait des erreurs dans la résolution.
Voici la méthode que tu as utilisée:
Tu as partitionné R en 2 parties P1 et P2 et c'est ce que tu as développé dans 1), jusque là tout est bon.
Ensuite dans 2) tu as résolu l'inéquation pour x appartenant à P1 et tu as trouvé l'ensemble S1 comme solutions. Mais tu as oublié que tu as résolu l'inéquation dans P1 et non pas dans R. L'ensemble des solutions est donc S'1 = P1 inter S1.
Même remarque pour la 3), l'ensemble des solutions est S'2 = P2 inter S2.
Et l'ensemble des solutions de l'inéquation dans R est égal à l'ensemble des solutions dans P1, union, l'ensemble des solutions dans P2, soit S = S'1 U S'2
mrif a écrit:On ne peut pas transposer la formule de ton cours à ce cas et cette formule: |a|>=b si (-b>=a>=b et b=b est toujours vraie quelque soit a.
Revenons à ton exercice. Ta méthode est correcte, mais elle n'aboutit pas car tu as fait des erreurs dans la résolution.
Voici la méthode que tu as utilisée:
Tu as partitionné R en 2 parties P1 et P2 et c'est ce que tu as développé dans 1), jusque là tout est bon.
Ensuite dans 2) tu as résolu l'inéquation pour x appartenant à P1 et tu as trouvé l'ensemble S1 comme solutions. Mais tu as oublié que tu as résolu l'inéquation dans P1 et non pas dans R. L'ensemble des solutions est donc S'1 = P1 inter S1.
Même remarque pour la 3), l'ensemble des solutions est S'2 = P2 inter S2.
Et l'ensemble des solutions de l'inéquation dans R est égal à l'ensemble des solutions dans P1, union, l'ensemble des solutions dans P2, soit S = S'1 U S'2
Donc ce que je peux faire c'est :
-b>=|a|>=b avec b>=0 et b<=0 pour avoir tous les cas possibles ?
pluie2 a écrit:Donc ce que je peux faire c'est :
-b>=|a|>=b avec b>=0 et b<=0 pour avoir tous les cas possibles ?
Non et en plus ça ne t'avance à rien à chercher dans cette direction car on ne connait pas le signe de b.
Essaie plutôt de corriger ce que tu as déjà fait car tu as déjà fait le gros du travail.
Essaie de trouver S'1 ensuite S'2 et enfin S.
mrif a écrit:Non et en plus ça ne t'avance à rien à chercher dans cette direction car on ne connait pas le signe de b.
Essaie plutôt de corriger ce que tu as déjà fait car tu as déjà fait le gros du travail.
Essaie de trouver S'1 ensuite S'2 et enfin S.
1) Etude de x²+x-4: x²+x-4>0 sur ]-oo; (-1-rac17)/2[U](-1+rac17)/2;+oo[ et x²+x-4= 2x-1 est équivalent à x²+x-4>=2x-1. Soit x²-x-3>=0. Les solutions sont donc ici : S1=]-oo;(1-rac13)/2[U](1+rac13)/2;+oo[.
3) Pour x appartient à ](-1-rac17)/2;(-1+rac17)/2[, |x²+x-4|>= 2x-1 équivaut à -x²-x+4>= 2x-1 soit -x²-3x+5>=0 donc S2=](-3-rac29)/2;-3+rac29/2[.
Donc : 2) S1=]-oo;(1-rac13)/2[U](1+rac13)/2;+oo[. et S2=](-3-rac29)/2;-3+rac29/2[.
je ^rends l'intersection des deux ? désolé j'ai un pe de mal avec toutes les notations notamment entre les P1, P2, S'1 et S'2...
pluie2 a écrit:1) Etude de x²+x-4: x²+x-4>0 sur ]-oo; (-1-rac17)/2[U](-1+rac17)/2;+oo[ et x²+x-4= 2x-1 est équivalent à x²+x-4>=2x-1. Soit x²-x-3>=0. Les solutions sont donc ici : S1=]-oo;(1-rac13)/2] U [(1+rac13)/2;+oo[.
3) Pour x appartient à ](-1-rac17)/2;(-1+rac17)/2[, |x²+x-4|>= 2x-1 équivaut à -x²-x+4>= 2x-1 soit -x²-3x+5>=0 donc S2=](-3-rac29)/2;-3+rac29/2[.
Donc : 2) S1=]-oo;(1-rac13)/2[U](1+rac13)/2;+oo[. et S2=](-3-rac29)/2;-3+rac29/2[.
je ^rends l'intersection des deux ? désolé j'ai un pe de mal avec toutes les notations notamment entre les P1, P2, S'1 et S'2...
Pour trouver les intersections et les unions tu utilises la droite réelle sur laquelle tu positionnes les différents intervalles:
P1 = ]-oo; (-1-rac17)/2] U [(-1+rac17)/2;+oo[
P2 = ](-1-rac17)/2;(-1+rac17)/2[.
S'1 = P1 inter S1 = ]-oo; (-1-rac17)/2] U [(1+rac13)/2;+oo[
Tu trouveras de la même façon S'2 = ](-1-rac17)/2 ; (-3+rac29)/2]
Donc S = S'1 U S'2 = ]-oo; (-3+rac29)/2] U [(1+rac13)/2;+oo[
pluie2 a écrit:pourquoi faut il élever au carré ?
c'est toujours bien de connaître plusieurs méthodes.
L'inéquation est donc |x²+x-4|>=2x-1
Une valeur absolue étant toujours positive, l'inégalité sera toujours vraie si 2x-10
on sait que des nombres positifs sont rangés dans le même ordre que leurs carrés.
|x²+x-4|²>=(2x-1)²
on peut remplacer les valeurs absolues par des parenthèses, ce qui simplifie la suite, car on a toujours |u|²=u² quel que soit u.
(x²+x-4)²>=(2x-1)²
(x²+x-4+2x-1)(x²+x-4-2x+1)>=0
(x²+3x-5)(x²-x-3)>=0
on se ramène à l'étude de signe de trinômes
pour x²+3x-5,
pour x²-x-3,
Le plus simple est de faire un tableau de signes (on est dans le cas où x>1/2).
Dans chaque cas, le coefficient de x² est positif, les trinômes sont positifs à l'extérieur des racines.

En ajoutant les valeurs infétieures à 1/2, on obtient comme ensemble de solutions:
S=
pluie2 a écrit:D'accord je vais refaire mais n'y a t il pas une méthode générale qui marche à tous les coups ?
Ta méthode et la méthode développée par chan79 sont des méthodes générales puisqu'elles marchent à coup sûr pour toute équation de la forme |f(x)| >= g(x).
Ta méthode se base sur le signe de f(x) et elle conduit à résoudre l'inéquation dans 2 domaines: le domaine P1 où f est positive et le domaine P2 où f est négative. Celle de chan79 se base sur le signe de g(x) et elle conduit elle aussi à résoudre l'équation dans 2 domaines: le domaine P'1 où g est positive et le domaine P'2 où g est négative.
chan79 a écrit:c'est toujours bien de connaître plusieurs méthodes.
L'inéquation est donc |x²+x-4|>=2x-1
Une valeur absolue étant toujours positive, l'inégalité sera toujours vraie si 2x-10
on sait que des nombres positifs sont rangés dans le même ordre que leurs carrés.
|x²+x-4|²>=(2x-1)²
on peut remplacer les valeurs absolues par des parenthèses, ce qui simplifie la suite, car on a toujours |u|²=u² quel que soit u.
(x²+x-4)²>=(2x-1)²
(x²+x-4+2x-1)(x²+x-4-2x+1)>=0
(x²+3x-5)(x²-x-3)>=0
on se ramène à l'étude de signe de trinômes
pour x²+3x-5,=29 ce trinôme s'annulle pour
qui est négatif et
égal environ à 1,19
pour x²-x-3,=13 ce trinôme s'annulle pour
qui est négatif et
égal environ à 2.3
Le plus simple est de faire un tableau de signes (on est dans le cas où x>1/2).
Dans chaque cas, le coefficient de x² est positif, les trinômes sont positifs à l'extérieur des racines.
En ajoutant les valeurs infétieures à 1/2, on obtient comme ensemble de solutions:
S=
j'ai refait mais moi je trouve des solutions différentes soit S=]-oo;(-3-rac29)/2[U](1+rac13)/2;+oo[ car on veut que (x²+3x-5)(x²-x-3) soit plus grand que 0 donc positif
chan79 a écrit:Salut
Revois les démonstrations proposées.
0 fait partie des solutions
ça y est je crois que j'ai compris.
Mais pour être totalement sure, à chaque fois que j'ai ce type d'inéquations, je peux toujours passer sur la résolution de 2x-1<=0 ou dans le cas général b<=0 car une valeur absolue est toujours positive donc sera toujours supérieure ?
pluie2 a écrit:ça y est je crois que j'ai compris.
Mais pour être totalement sure, à chaque fois que j'ai ce type d'inéquations, je peux toujours passer sur la résolution de 2x-1<=0 ou dans le cas général b<=0 car une valeur absolue est toujours positive donc sera toujours supérieure ?
Histoire de s'entraîner, je te propose de résoudre: |x+1|<x+2 :zen:
[quote="chan79"]Histoire de s'entraîner, je te propose de résoudre: |x+1|0
-x-2<x+1 donc -2x-3<0 et x+1<x+2 vrai sur R.
Donc :
-2x-3 s'annule quand x=-3/2 donc sur ]-oo;-3/2[, -2x-3 est positif et sur ]-3/2;+oo[ négatif.
x+2 s'annue quand x=-2 donc je fais l'intersection des deux ensembles et je trouve ]-3/2;+oo[.
C'est louche car ce n'est pas ce que j'pbtiens à la calculatrice... :doh:
-x-2<x+1 donc -2x-3<0 et x+1<x+2 vrai sur R.
Donc :
-2x-3 s'annule quand x=-3/2 donc sur ]-oo;-3/2[, -2x-3 est positif et sur ]-3/2;+oo[ négatif.
x+2 s'annue quand x=-2 donc je fais l'intersection des deux ensembles et je trouve ]-3/2;+oo[.
C'est louche car ce n'est pas ce que j'pbtiens à la calculatrice... :doh:
pluie2 a écrit:Ok donc :
|x+1|0
-x-2<x+1 donc -2x-3<0 et x+1<x+2 vrai sur R.
Donc :
-2x-3 s'annule quand x=-3/2 donc sur ]-oo;-3/2[, -2x-3 est positif et sur ]-3/2;+oo[ négatif.
x+2 s'annue quand x=-2 donc je fais l'intersection des deux ensembles et je trouve ]-3/2;+oo[.
C'est louche car ce n'est pas ce que j'pbtiens à la calculatrice... :doh:
ton résultat est correct
Quel est le problème avec la calculatrice ?
38 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 35 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
