Inégalité vraie sur R+

[marawita1]

Bonsoir,
J'ai une petite question: j'ai l' inégalité suivante:
Pour tout b>0 , f(t)<= A pour tout t dans [0, b] (peu n'importe f et A), ma question comment je peux déduire que cette dernière inégalité est vraie pour tout t dans ?

Merci d'avance.

[Robot]

Tu n'as pas précisé la quantification sur le (c'est essentiel !).

Est-ce que c'est

ou alors

?

Si c'est bien le 1er cas de figure, tu choisis tel que

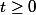
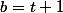
est vrai. Soit alors . Prends et conclus.

[marawita1]

C'est bien le premier cas. Soit t>= 0 , on choisit b=t+1>0, donc f(b)= f(t+1)<=A, et après?

Franchement j'ai pas bien saisi votre méthode!!!!!!

[Robot]

Oui, je vois que tu es passé à côté (je souligne là où tu passes à côté).

C'est bien le premier cas. Soit t>= 0 , on choisit b=t+1>0, donc f(b)= f(t+1)<=A, et après?

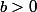
On a , on a , donc ...

[marawita1]

Oui, je vois que tu es passé à côté (je souligne là où tu passes à côté).

C'est bien le premier cas. Soit t>= 0 , on choisit b=t+1>0, donc f(b)= f(t+1)<=A, et après?

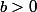
On a , on a , donc ...

donc f(t) <=A, c'est ça?
Si c'est bien ça, j'ai pas compris l'utilité de choisir b=t+1!!!!!!

[Robot]

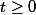
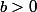
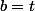
On aurait pu choisir . Ou alors . Ca n'a aucune importance, la seule chose qui compte, une fois qu'on s'est donné , c'est de choisir tel que et ; prendre n'irait pas car on peut avoir .

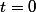
[marawita1]

ok merci très bien.