F^-1(x) dans f-1(A) => x dans A, réciproque vraie?
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
skyskiper
- Membre Relatif
- Messages: 155
- Enregistré le: 08 Oct 2005, 21:16
-
 par skyskiper » 09 Nov 2006, 20:07
par skyskiper » 09 Nov 2006, 20:07
Salut à tous!
Aujourd'hui, je me suis posé
une petite question en révisant mon cours de logique. Si quelqu'un pouvait m'éclairer, ce serait super sympa!
Voilà, je sais que:
 \in f^{-1}(A) \Rightarrow x \in A)
Mais a-t-on la réciproque? C'est à dire:
 \in f^{-1}(A))
En gros, a-t-on?
 \in f^{-1}(A) \Leftrightarrow x \in A)
Merci à tous ceux qui prendront un peu de leur temps pour me répondre! :we:
++
-
skyskiper
- Membre Relatif
- Messages: 155
- Enregistré le: 08 Oct 2005, 21:16
-
 par skyskiper » 09 Nov 2006, 21:03
par skyskiper » 09 Nov 2006, 21:03
Personne ne sait?
Si quelqu'un a la réponse, je veux bien qu'il me la donne parce que j'ai une interro de maths demain... :triste:
Merci d'avance!
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 09 Nov 2006, 21:09
par Zebulon » 09 Nov 2006, 21:09
Bonsoir,
skyskiper a écrit:Mais a-t-on la réciproque? C'est à dire:
 \in f^{-1}(A))
c'est vrai si x admet un antécédent par f.
Ce qui est vrai, sans condition, c'est :
\subseteq f^{-1}(A))
.
-
abcd22
- Membre Complexe
- Messages: 2426
- Enregistré le: 13 Jan 2006, 14:36
-
 par abcd22 » 09 Nov 2006, 21:10
par abcd22 » 09 Nov 2006, 21:10
Bonsoir,
Qu'est-ce que tu appelles

?
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 09 Nov 2006, 21:11
par Zebulon » 09 Nov 2006, 21:11
Je pense que c'était des
)
, non ?
-
skyskiper
- Membre Relatif
- Messages: 155
- Enregistré le: 08 Oct 2005, 21:16
-
 par skyskiper » 09 Nov 2006, 21:12
par skyskiper » 09 Nov 2006, 21:12
C'est une erreur de frappe, escusez moi.
Je l'ai corrigé. :we:
-
skyskiper
- Membre Relatif
- Messages: 155
- Enregistré le: 08 Oct 2005, 21:16
-
 par skyskiper » 09 Nov 2006, 21:15
par skyskiper » 09 Nov 2006, 21:15
Donc si j'ai bien compris, si x admet un antécédent par f, alors l'équivalence est vraie. C'est ça?
-
abcd22
- Membre Complexe
- Messages: 2426
- Enregistré le: 13 Jan 2006, 14:36
-
 par abcd22 » 09 Nov 2006, 21:21
par abcd22 » 09 Nov 2006, 21:21
)
(notation abusive pour
)
) est un ensemble (donc on ne peut pas dire «
 \in f^{-1}(A))
» mais
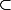
), sauf si on suppose f bijective.
-
skyskiper
- Membre Relatif
- Messages: 155
- Enregistré le: 08 Oct 2005, 21:16
-
 par skyskiper » 09 Nov 2006, 21:24
par skyskiper » 09 Nov 2006, 21:24
Oui, je n'ai pas précisé que f était bijective, escusez moi...
J'ai beaucoup de mal avec ce genre de logique mathématique... :triste:
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 09 Nov 2006, 21:27
par Zebulon » 09 Nov 2006, 21:27
skyskiper a écrit:Donc si j'ai bien compris, si x admet un antécédent par f, alors l'équivalence est vraie. C'est ça?
Oui, mais sans condition, on a l'équivalence
\subseteq f^{-1}(A))
.
En effet,
soit f :

une application et

, alors
\subseteq f^{-1}(A)\ \Longleftrightarrow\ \forall y\in f^{-1}(\{x\}),\ y\in f^{-1}(A)\\<br />\Longleftrightarrow\ [\forall y\in X,\ f(y)\in \{x\}\ \Rightarrow\ f(y)\in A]\\<br />\Longleftrightarrow\ [\forall y\in X,\ f(y)=x\ \Rightarrow\ f(y)\in A]\\<br />\Longleftrightarrow\ x\in A)
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 09 Nov 2006, 21:33
par Zebulon » 09 Nov 2006, 21:33
Skyskiper a écrit:Donc si j'ai bien compris, si x admet un antécédent par f, alors l'équivalence est vraie. C'est ça?
Zebulon a écrit:Oui
Non ! :we:
)
n'a de sens que si f est bijective, pas même si x admet un unique antécédant.
Ici, c'est le cas, OK. Mais c'était une erreur de ma part. En revanche, l'équivalence de mon dernier post est juste quelle que soit f.
-
skyskiper
- Membre Relatif
- Messages: 155
- Enregistré le: 08 Oct 2005, 21:16
-
 par skyskiper » 09 Nov 2006, 21:37
par skyskiper » 09 Nov 2006, 21:37
Donc, si je récapitule la chose:
Si f est bijective, alors l'équivalence que j'ai posé dans mon premier post est vraie, c'est ça?
Merci
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 09 Nov 2006, 21:45
par Zebulon » 09 Nov 2006, 21:45
Oui, puisque si f est bijective,
=\{f^{-1}(x)\})
donc l'équivalence :
\subseteq f^{-1}(A))
s'écrit :
\}\subseteq f^{-1}(A))
qui est équivalente à
\in f^{-1}(A))
.
-
skyskiper
- Membre Relatif
- Messages: 155
- Enregistré le: 08 Oct 2005, 21:16
-
 par skyskiper » 09 Nov 2006, 21:52
par skyskiper » 09 Nov 2006, 21:52
Oki, merci bien! :lol4:
Il me reste une question: (f est toujours bijective)
 \Rightarrow f^{-1}(x) \in A)
Mon prof m'a dit que cette implication est fausse, mais je ne comprend pas pourquoi... Peux-tu m'expliquer? (avec un contre exemple si possible...)
Merci d'avance! :we:
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 09 Nov 2006, 21:59
par Zebulon » 09 Nov 2006, 21:59
Il faut préciser les hypothèses. f est-elle une application de A dans Y ? De X dans Y avec

? Et dans ce cas, f est-elle bijective de X sur Y ? Seulement de A sur f(A) ? etc...
-
skyskiper
- Membre Relatif
- Messages: 155
- Enregistré le: 08 Oct 2005, 21:16
-
 par skyskiper » 09 Nov 2006, 22:05
par skyskiper » 09 Nov 2006, 22:05
Je pense que je vais abandonner pour ce soir.
Je suis vraiment pas à l'aise avec ces trucs là...
En plus je commence vraiment à être crevé... lol!
Bon bah je crois que y'a plus qu'à compter sur ma bonne étoile pour qu'il n'y ait pas ce genre de truc dans mon interro de demain...
Enfin en tout cas, merci à vous deux Zebulon et abcd22.
Passez un bonne soirée et bon remuménage de neuronnes! lol
Merci! :we:
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 09 Nov 2006, 22:21
par Zebulon » 09 Nov 2006, 22:21
Moi aussi je vais aller me coucher, mais avant je vous explique ça :
si

est bijective, et

, alors
\ \Rightarrow\ \left\{x\in Y\\x\in f(A)\ \Rightarrow\ \left\{\exists!y\in X\ f(y)=x\\y\in A)
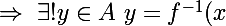\\<br />\Rightarrow\ f^{-1}(x)\in A)
.
Donc, dans ce cas, c'est vrai.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 32 invités
