Incompréhension du cours (sur les anneaux)
17 messages
- Page 1 sur 1
Incompréhension du cours (sur les anneaux)
Bonsoir, mes questions concerneront mon cours :s, j'ai des bouts comme ça et je ne sais pas à quoi ça correspond..
J'ai alpha = xy.(x+y) = xyx+xy²
= xxy+xy²
= x²y+xy²
= xy+yx
= 0
Pourquoi est-ce égal à 0 lorsqu'on a simplifié?
sinon, Quelque soit (x,y) appartient à A² (c'est la suite)
xy(x+y)=0 XY = 0
On dit que l'anneau n'est pas intègre...
Je n'ai pas compris :s?
merci d'avance pour vos explications
bonne soirée
J'ai alpha = xy.(x+y) = xyx+xy²
= xxy+xy²
= x²y+xy²
= xy+yx
= 0
Pourquoi est-ce égal à 0 lorsqu'on a simplifié?
sinon, Quelque soit (x,y) appartient à A² (c'est la suite)
xy(x+y)=0 XY = 0
On dit que l'anneau n'est pas intègre...
Je n'ai pas compris :s?
merci d'avance pour vos explications
bonne soirée
Aille
Tu penses pas qu'il manque un ptit détail sur l'anneau en question ?
J'suppose que c'est l'anneau de Boole comme dans l'autre post ?
Tout se joue sur la commutativité :^)
Sinon un anneau est intégre quand il n'a pas de diviseur de zéro
Autrement dit si pour tout x,y A : xy = 0 => x = 0 ou y = 0
Goue d'baille
Tu penses pas qu'il manque un ptit détail sur l'anneau en question ?
J'suppose que c'est l'anneau de Boole comme dans l'autre post ?
Tout se joue sur la commutativité :^)
Sinon un anneau est intégre quand il n'a pas de diviseur de zéro
Autrement dit si pour tout x,y A : xy = 0 => x = 0 ou y = 0
Goue d'baille
J'ai alpha = xy.(x+y) = xyx+xy²
là on a juste développé
= xxy+xy²
On a utilisé la commutativité xyx=xxy
= x²y+xy²
xx=x²
= xy+yx
c'est un anneau de boole donc x²=x et y²=x
En fait, on trouve xy+yx mais comme la loi + est commutative ça revient au même
= 0
Là, il y a deux étapes:
alpha=xy+xy par commutativité
= 0 parce que x+x=0 quel que soit x
un diviseur de 0 c'est un élément, autre que 0 qui donne 0 quand on le multiplie par autre chose.
En clair si A.B=0 et que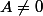 et
et 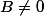 alors A et B sont des diviseurs de 0.
alors A et B sont des diviseurs de 0.
Par définition, un anneau intègre est un anneau qui n'a pas de diviseurs de 0.
Or, ici on trouvé que pour tout x et y, xy.(x+y)=0
xy et x+y ne sont pas égaux à 0, on a donc bien trouvé des diviseurs de 0 et l'anneau de Boole n'est donc pas intègre.
En clair si A.B=0 et que
Par définition, un anneau intègre est un anneau qui n'a pas de diviseurs de 0.
Or, ici on trouvé que pour tout x et y, xy.(x+y)=0
xy et x+y ne sont pas égaux à 0, on a donc bien trouvé des diviseurs de 0 et l'anneau de Boole n'est donc pas intègre.
Il y a effectivement deux lois + et .
+ est associative ( a+(b+c) = (a+b)+c) et commutative (a+b=b+a)
. est associative et distributive par rapport à + c'est à dire a(b+c) = ab+ac
Par contre, il n'y a aucune obligation à ce que la loi . soit commutative.
Si t'as encore des questions n'hésite pas (j'espère que je saurais y répondre)
+ est associative ( a+(b+c) = (a+b)+c) et commutative (a+b=b+a)
. est associative et distributive par rapport à + c'est à dire a(b+c) = ab+ac
Par contre, il n'y a aucune obligation à ce que la loi . soit commutative.
Si t'as encore des questions n'hésite pas (j'espère que je saurais y répondre)
17 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 85 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
