Identifier une somme de Riemann
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Jfmamjjasond2
- Membre Naturel
- Messages: 33
- Enregistré le: 02 Mar 2010, 18:45
-
 par Jfmamjjasond2 » 06 Avr 2010, 20:26
par Jfmamjjasond2 » 06 Avr 2010, 20:26
Hello,
j'ai un TD avec plein de suites dont je dois calculer la limite, et où l'énoncé dit explicitement d'utiliser les sommes de Riemann. Sauf que j'ai un mal fou à identifier ce qui dans
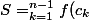(a_{k+1}-a_k))
représente la subdivision, la fonction et la famille
_{k \in [1;n]})
.
Y a-t-il une méthode systèmatique pour identifier tout ça dans une somme donnée où alors c'est toujours au feeling (auquel cas je suis mal barré) ?
Merci d'avance pour votre aide.
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 06 Avr 2010, 20:44
par girdav » 06 Avr 2010, 20:44
Bonsoir,
on peut s'en sortir dans le cas classique où l'on fait la subdivision de l'intervalle
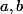
en prenant les points de la forme
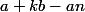
avec
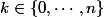
. Et encore, on prends souvent l'intervalle
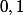
.
Si tu as quelques exemple histoire de voir si ça se confirme.
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 07 Avr 2010, 08:58
par girdav » 07 Avr 2010, 08:58
En fait il y a toujours un bricolage pour se ramener à
)
. Par exemple, pour la première, on a
^2})
.
-
Jfmamjjasond2
- Membre Naturel
- Messages: 33
- Enregistré le: 02 Mar 2010, 18:45
-
 par Jfmamjjasond2 » 07 Avr 2010, 21:41
par Jfmamjjasond2 » 07 Avr 2010, 21:41
Donc si j'ai bien compris, fondamentalement dans les exos j'aurais toujours affaire à un truc de la forme
)
, où il se peut que j'en ai d'autres ?

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 07 Avr 2010, 21:51
par Ben314 » 07 Avr 2010, 21:51
A mon avis, je pense que tu auras quasiement exclusivement ce type là qui correspond à une subdivision régulière de l'intervalle [a,b].
Je pense même que, vu que toute intégrale de a à b peut, à l'aide d'un changement de variable, se ramener à une intégrale de 0 à 1 qu'il faut t'attendre à n'avoir quasi que des sommes du type :
)
qui, si
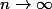
tendent vers
dt)
Tes 4 exemples sont de ce types à la "mini-variante" prés que, si k varie de 1 à n ou bien de 0 à n ou bien de 1 à n-1, et bien... ça ne change rien car les 1 ou 2 termes en plus (ou en moins) tendent vers 0.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 208 invités
