Presque une somme de Riemann
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
 par busard_des_roseaux » 24 Mar 2008, 17:42
par busard_des_roseaux » 24 Mar 2008, 17:42
Bjr,
Pour une fonction régulière, la somme de Riemann
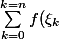 (x_{k}-x_{k-1}))
approche le nombre:
dt)
Dans les m^mes conditions, comment traiter une somme de la forme:
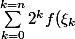 (x_{k}-x_{k-1}))
Je n'ai pas trop d'idée ?

-
nuage
- Membre Complexe
- Messages: 2214
- Enregistré le: 09 Fév 2006, 22:39
-
 par nuage » 24 Mar 2008, 18:40
par nuage » 24 Mar 2008, 18:40
Salut,
 \text{d}t})
en remplaçant

par

.
Sinon c'est sévèrement divergent, prendre par exemple
=1)
et
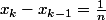
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 24 Mar 2008, 18:41
par ThSQ » 24 Mar 2008, 18:41
il y a surement une réponse dans des cas particuliers.
En tout cas si f(x) = 1, x^n, ... sur 0..1, avec une distribution k/n, la limite est +°° (+ généralement toute fonction > 0 et croissante).
 par busard_des_roseaux » 25 Mar 2008, 05:21
par busard_des_roseaux » 25 Mar 2008, 05:21
merçi à vous deux, je vais regarder ce que je peux faire suite à vos réponses.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 53 invités