Groupes

[yos]

Bonjour.
Voilà un exercice pour lequel j'ai mis deux plombes à trouver la solution, donc vous n'êtes pas obligé de trouver en cinq minutes, sauf si vous tenez à me vexer.

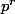
Soit G un groupe de cardinal (p premier), et H un sous-groupe distingué de cardinal p. Démontrer que .

[nonam]

Me trompe peut-etre :
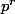
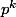
pour x dans H, l'ordre de l'orbite de x (pour l'action de conjugaison) divise , donc elle est de la forme . Mais comme cette orbite est incluse dans H puisqu'il est distingué, on a . Mais ca ne peut-etre p, sinon on aurait , et donc l'élément neutre e serait dans l'orbite de x, donx x= e et : contradiction...
Ainsi tout élément de H est fixe pour l'action de conjugaison, donc

[ThSQ]

Je pense que l'hypothèse que G est un p-groupe est superflue, je propose :

si |H|=p, H est normal dans G et p et le plus petit nombre premier divisant |G| alors H est dans le centre ( "le milieu c'est merveilleux et le centre y'a pas mieux" )

On reprend l'idée de nonam en utilisant la conjugaison mais en se plaçant dans Aut(H), d'ordre p-1 (connu : tout est déterminé par l'image d'un générateur).


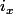
pour tout x dans H donc l'ordre de divise p-1 et |G|.

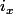
est bien définie sur H vu que H est distingué et c'est un automorphisme.


(laborieux ....)

[yos]

Bravo à vous.
J'ai fait la même chose que Nonam, mais j'avais d'abord trouvé un truc nettement plus compliqué.
Thsq, je comprends pas bien ton premier argument. Tu appliques p fois de suite l'automorphisme intérieur à un élément y donné de H ? Je suis fatigué, je regarderai ça demain.

[ThSQ]

Oui c'est pas super clair. J'essaierai de mettre ça au propre ce soir si c'est toujours pas clair.

[nonam]

Joli ThSQ !
Mais du coup, je vois pas bien à quoi sert l'hypothèse : plus petit nombre premier divisant |G| ?

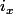
edit : en fait, apres réflexion, je comprends pas bien pq l'ordre de divise p-1...
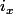
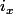
re-edit : compris en fait (je voyais comme élément de Aut(G)). Mais du coup après qd tu dis , tu considère comme automorphisme de G, et plus de H ? sinon on a meme vu que H est commutatif... bref, finalement, je patauge.

[ThSQ]

Pour le 1 : le seul nombre qui divise un nombre donnée et qui est plus petit que tous ses diviseurs c'est 1.

Pour le 2 : |Aut(H)| = p-1

[leon1789]

hé l'eau,

Je pense que l'hypothèse que G est un p-groupe est superflue, je propose :

si |H|=p, H est normal dans G et p et le plus petit nombre premier divisant |G| alors H est dans le centre

Oui, un poil plus général, en prenant |H|=p premier divisant |G| tel que pgcd(p-1, |G|)=1.

Je pensais aussi à , H cyclique d'ordre p premier,
donc
Mais après, est un automorphisme de G car pgcd(p-1,|G|)=1.
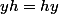
d'où pour tout

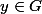
[leon1789]

Je pensais aussi à donc
Mais après, est un automorphisme de G car pgcd(p-1,|G|)=1.

[yos]

Mais du coup après qd tu dis ,[...]je patauge.

Moi aussi, mais pour poursuivre la métaphore aquatique, c'est peut-être parce que Thsq nous mène en bateau lorsqu'il confond et . Mais sa pensée a très bien pu m'échapper.

Sinon, Léon, pourquoi est un automorphisme de G? Je vois même pas pourquoi c'est un morphisme.

[leon1789]

Sinon, Léon, pourquoi est un automorphisme de G? Je vois même pas pourquoi c'est un morphisme.

, c'est multiplicatif ... ah ! oh ! J'ai pris G commutatif ... :doh: après, je m'étonne que H soit dans le centre :marteau: bon, je vais me coucher

[ffpower]

non?(x est dans H donc )

[yos]

x est dans H donc

Non : on a besoin de x dans G. C'est y qui est dans H.
La proposition de Léon est récupérable dans le cas du p-groupe moyennant le petit théorème de Fermat.

[leon1789]

Sinon, Léon, pourquoi est un automorphisme de G? Je vois même pas pourquoi c'est un morphisme.

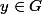
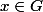
en fait, on s'en fiche que cela soit un morphisme (je me suis un peu emporté sur ce coup) , mais ce qui est important, c'est que cela soit une application bijective ! pour tout , il existe tel que . Il faut prendre où

Non ?

[ffpower]

Non : on a besoin de x dans G. C'est y qui est dans H.
La proposition de Léon est récupérable dans le cas du p-groupe moyennant le petit théorème de Fermat.

Ouai en fait c est plutot ou n est le cardinal de G..Mais c est suffisant pour conclure je pense(modulo le fait que Aut(H) est de cardinal p-1,me souvien plu tro de ces trucs la mais je crois que c est vrai)

[leon1789]

Soit H un sous-groupe cyclique et normal de G.
Si alors


H cyclique d'ordre n
donc Aut(H) est de cardinal (lié aux générateurs de H)
Pour tout ,
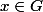
on note la conjugaison par x (bien défini car H normal),
donc
Or est une application bijective de G (mais pas un automorphisme :id: ), de réciproque où
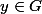
Ainsi, pour tout , on a .

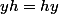
[ThSQ]

Bon, j'ai pas le temps de lire toute votre prose (l'appel du platal ....et accessoirement du DS à venir :peur: ), Léon semble avoir trouvé des généralisations élégantes.

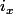
Mon idée est de considéré comme automorphisme dans H (défini biscotte distingué). Son ordre divise p-1 (biscotte |Aut(H)|=p-1) et aussi n (biscotte ) et le seul nombre qui divise p-1 et n c'est 1 et c'est fini.

Bon, c'est peut-être une monstrueuse stupidité et mon QI est surement celui d'un bigorneau mort (comme me le dit mon petit frère ...) mais là je vois pas le pb. J'arrête les maths et je me mets aux timbres-poste :help:

[leon1789]

Léon semble avoir trouvé des généralisations élégantes.

ben en fait, c'est quasi la même chose que toi.

[yos]

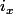
Mon idée est de considéré comme automorphisme dans H (défini biscotte distingué). Son ordre divise p-1 (biscotte |Aut(H)|=p-1) et aussi n (biscotte ) et le seul nombre qui divise p-1 et n c'est 1 et c'est fini.

Cette fois c'est OK et c'est ce qu'a écrit ffpower plus haut. Il me semble qu'avec ça marchait pas.

[ThSQ]

Ouais c'était une typo (p à la place de n), une de plus, sinon je vois pas comment j'aurais pu en déduire que l'ordre divisait p-1 et n ...