Fourier et équa-diff

[Ziradus50]

Bonsoir !
Je me demandais comment résoudre à l'aide d'une série de fourier l'équa diff suivante :

En passant par les coefficients de Fourier ( les cn(f) ) on obtient:

soit:
soit encore :



Comment procéder à partir de là ?
Merci

[Ziradus50]

up :) si quelqu'un a une idée :)

[mr_pyer]

On obtient si on pose dans ton équation.
Par ailleurs on obtient facilement la solution de l'équation homogène. On voit ainsi que l'on peut supposer pour la solution particulière. Cela donne et .

Ce qui m'embête c'est que le coefficient explose quand . Je crains que la solution ne soit pas une série de Fourier...

[Ziradus50]

Je crains que la solution ne soit pas une série de Fourier...

Pourtant c'est bien sous cette forme qu'il faut trouver y

[Ziradus50]

Un peu d'aide ? :)

[mr_pyer]

Je suis quasi sûr que la solution n'est pas périodique.
La suite est censé être dans (même en fait), ici ça n'est clairement pas le cas.
Par contre on peut résoudre l'équa-diff plus ou moins facilement de manière classique...

[JeanJ]

Je suis quasi sûr que la solution n'est pas périodique.
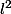
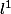
La suite est censé être dans (même en fait), ici ça n'est clairement pas le cas.
Par contre on peut résoudre l'équa-diff plus ou moins facilement de manière classique...

Bien sûr que mr_pyer a raison. On ne peut pas représenter les solutions de l'équation différentielle sous forme de série de Fourier pour tout x de -infini à +infini.
C'est aussi impossible que de demander, par exemple, de représenter la fonction y(x)=x² sous forme de série de Fourier pour tout x de -infini à +infini. Ce qui est classiquement demandé est de représenter cette fonction sur un intervalle donné (par exemple pi<x<pi, ou autre) La série de Fourier que l'on sait calculer coïncide bien avec y=x² sur l'intervalle spécifié, mais pas hors de cet intervalle : pour x tendant vers l'infini, la série poursuit son comportement périodique, alors que la fonction initiale y=x² tend vers l'infini.
Il faut en conclure que l'énoncé du problème est : soit mal posé (pour une raison inconnue : mauvaise transcription, coquille dans l'équation, etc.) , soit incomplet (intervalle non spécifié).

On peut aussi se demander s'il s'agit vraiment d'une question sur les séries de Fourier ? Est-ce que, par hasard, la question serait de rechercher s'il est possible de résoudre l'équation différentielle grâce à la transformation de Fourier? Ce qui n'est pas du tout la même chose !
Mais, comme le dit très justement mr_pyer, on sait la résoudre par méthode plus classique (bien que le résultat analytique fasse intervenir une fonction spéciale).

[Ben314]

Salut,
Si on résoud "bètement" l'équa. diff. (équation homogène + variation de la constante) on trouve que où .
La fonction est périodique ssi l'est, c'est à dire ssi .
(=cercle trigo).
(en utilisant les résiduts)

Donc effectivement, la fonction n'est pas périodique...
Remarque :
1) On peut aussi calculer avec des outils plus rudimentaires en écrivant que
2) Le fait que montre que la fonction est périodique et donc que l'est aussi et que cette fonction est solution de l'équa.diff.