Rik95 a écrit:Merci Bianco

Un ami ma fait parvenir la correction de son prof de TD, je viens de regarder pour les 2 premiers que j'ai essayer de faire donc celle la et une autre ou il faut montrer que e^x > x+1 pour tout x appartenant a R étoile.
Dans les 2 cas le prof a directement considérer qu'il y'avais un C dans l'intervalle donnée ... donc pour la première il a considéré qu'il y'avais un C dans ]0, + l'infini[ or d'apres ma comprehension vu qu'on a x > 0 donc x >= 1 on devrait conciderer le C dans l'intervalle ]1, + l'infini [ ...
meme chose dans la 2eme on a R etoile, il a supposer qu'on avait C dans ] 0, + l'infini [ et il a démontrer le résultat dans cet intervalle puis il a supposer C dans ] - l'infini, 0 [ or on devrait prendre C dans ] 1, + l'infini [ .. etc non ?
Est ce que j'ai mal compris le principe lorsque l'on considère le C dans l'intervalle ?
En fait, tout dépend si tu utilises le théorème pour une égalité, à savoir qu'il existe
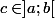
(logique, on considère que c'est au moins dérivable sur l'ouvert) tel que :
= \frac{f(b)-f(a)}{b-a})
Ensuite, c'est que si on a un encadrement de la dérivée, c'est à dire :
 \leq k)
, on aura :
-f(a)}{b-a}| \leq k)
, sauf que, cette inégalité fonctionne donc aussi sur tous les intervalles inclus dans
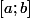
... (vu la définition du

).
Donc, finalement, si tu prends

, tu auras :
-f(x)}{y-x}| \leq k)
( on a bien [x;y] inclus dans [a;b]).
Dans notre exemple, avec la fonction ln, x+1 et 0 sont bien sur
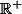
, donc tout va bien !
C'est ce que tu "mets" dans f qui doit être dans l'intervalle de départ de majoration de la dérivée :lol3:
