Accroissement fini et rolle ...

par **MacErmite** » 15 Déc 2009, 00:31

Bonsoir,

je cherche à démontrer l'égalité suivante

mais je ne vois pas comment commencé .

Pouvez-vous m'éclairer ?

Merci

par **Nightmare** » 15 Déc 2009, 01:07

Tu pourrais commencer par donner des hypothèses :lol3:

par **alavacommejetepousse** » 15 Déc 2009, 04:41

bonjour

pour f C2 sur [a,b]

deux fois FTL et une fois TVI

par **lapras** » 15 Déc 2009, 06:22

Je pense qu'il veut dire : soient a et b... il existe c tel que :

par **MacErmite** » 15 Déc 2009, 06:49

Oui en effet, f est une fonction deux fois dérivable sur [a,b] avec c appartenant à cet interval.

PS. : Savez-vous pourquoi je ne peux pas ré éditer des formules TEX après avoir effectué une prévisualisation, car elles sont générées en images impossibles à modifier.

par **Ben314** » 15 Déc 2009, 10:05

Bonjour
Peut-être pourrait tu appliquer le théorème de Taylors à la fonction

où

...
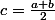
Attention : une dérivée n'est pas forcément continue... mais elle vérifie toujours le théorème des valeurs intermédiaires...

P.S. : il y a sans doute plus simple, mais je ne vois pas...

par **Zweig** » 15 Déc 2009, 17:23

Salut,

Je ne pense pas que MacErmite ait vu le théorème de Taylor (cf : les théorèmes cités dans le sujet).

On pose

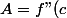et

Clairement,

. On choisit

de sorte que

. Clairement,

est continue sur [a, b] et dérivable sur ]a, b[ (comme

l'est). D'après le théorème de Rolle, il existe

tel que :

Conclus en utilisant le théorème des valeurs intermédiaires.

par **MacErmite** » 15 Déc 2009, 21:08

Zweig a écrit:Salut,

Je ne pense pas que MacErmite ait vu le théorème de Taylor (cf : les théorèmes cités dans le sujet).

On pose et

Clairement,. On choisit de sorte que . Clairement, est continue sur [a, b] et dérivable sur ]a, b[ (comme l'est). D'après le théorème de Rolle, il existe tel que :

Conclus en utilisant le théorème des valeurs intermédiaires.

Merci pour tout ces détails mais même avec différents cours sous les yeux je ne voi absolument rien. Géométriquement, devant un graph, je comprends le théoreme de Roll. Mais appliquer celui des accroissements finis avec la création d'une fonction auxilliaire, là je décroche...

Comment as-tu fais pour écrire \phi '

par **Ben314** » 15 Déc 2009, 21:43

Comprend tu quand même la preuve de Zweig ?
(je pense que le on pose A=... est de trop dans la preuve)
Le th. de Rolles et le Th. des Accroissements Finis sont assez façiles à visualiser, mais il y a beaucoup d'exercices les concernant qui demandent un peu d'astuce... Celui là en fait clairement parti.

Si tu veux en chercher un moins dur (mais où il faut trouver une fonction "intermédiaire"), je me rappelle de celui ci :
Soit f une fonction dérivable sur [0,1[ telle que f(0)=f(1)=f'(0).
Montrer qu'il existe c dans ]0,1[ tel que la tangente à la courbe au point d'abscice c passe par l'origine.

par **MacErmite** » 15 Déc 2009, 21:53

Ma difficulté est que je bloque sur la création de phi, fonction auxiliaire

pour vérifier les hypothèses du théorème de Rolle
phi(x)= .

. avec a et b tel que phi(a)=phi(b) et ainsi l'on a un point C tel que phi ' (c) = 0

par **Ben314** » 15 Déc 2009, 22:04

Bon, je me permet de "rerédiger" la preuve de Zweig (y va pas être content... :doh: ):

Zweig a écrit:On considère la fonction où A est le réel tel que
Cela signifie que l'on a pris (mais... on s'en fiche pour la suite)

Clairement, est continue sur [a, b] et dérivable sur ]a, b[ et .
D'après le théorème de Rolle, il existe tel que :

Conclus en utilisant le théorème des accroissements finis.

par **Nightmare** » 15 Déc 2009, 22:19

Personne a une idée "géométrique" ? Ca ressemble à de la convexité.

par **MacErmite** » 15 Déc 2009, 22:26

Comment fais t on pour obtenir cette dérivée ?

par **Ben314** » 15 Déc 2009, 22:30

MacErmite a écrit:Comment fais t on pour obtenir cette dérivée ?

Ben.., je dérive bétement : A est une constante et la dérivée de f(ax+b) est a.f'(ax+b)...

Pour Nightmare, tu parle de l'exo de départ ?

par **Nightmare** » 15 Déc 2009, 22:33

Oui ! :happy3:

par **Ben314** » 15 Déc 2009, 22:40

Nightmare,
Il me semble que la convexité te dit juste que le terme "final" (i.e. le A de la preuve de zweig) est du signe de f'' (si f'' ne change pas de signe) mais je ne vois pas comment elle te donnerais la valeur de A directement...
J'ai plutôt l'impression que cela marche "dans l'autre sens" i.e. que l'égalité demandée montre (presque) que (f''>0 => f convexe).

par **Ben314** » 15 Déc 2009, 22:43

Euhhhhh, MacHermite,
Si ce qui te surprend dans la formule de la dérivée est que l'on a pas dérivé f,.... et bien tu as parfaitement raison : c'est

Désolé.... (mais c'est uniquement une faute de frappe : cela ne remet pas en cause du tout la preuve..)

par **MacErmite** » 15 Déc 2009, 22:47

Ben314 a écrit:Euhhhhh, MacHermite,
Si ce qui te surprend dans la formule de la dérivée est que l'on a pas dérivé f,.... et bien tu as parfaitement raison : c'est

Désolé.... (mais c'est uniquement une faute de frappe : cela ne remet pas en cause du tout la preuve..)

ok pour f ' (x)/2 pour -A(...) mais je ne comprends pas celui du milieu : pourquoi diviser par 2 ?

par **Ben314** » 15 Déc 2009, 22:51

C'est justement la régle de dérivation d'une composée de deux fonction qui dit que la dérivée de x->f(ax+b) est x->a.f'(ax+b)
et ici, a=1/2...

par **MacErmite** » 15 Déc 2009, 23:30

Ben314 a écrit:C'est justement la régle de dérivation d'une composée de deux fonction qui dit que la dérivée de x->f(ax+b) est x->a.f'(ax+b)
et ici, a=1/2...

je viens juste de comprendre : x ---> ax+b ---> f (ax+b) avec la forme générale (gOf)'(x) = g'(f(x)).f'(x)

Mais pour le reste, je plane et l'enervement aidant je crois que tout va passé par la fenêtre.

Accroissement fini et rolle ...

Accroissement fini et rolle ...

Qui est en ligne