Formule du binôme
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
mostdu95
- Membre Relatif
- Messages: 436
- Enregistré le: 09 Sep 2006, 17:36
-
 par mostdu95 » 30 Oct 2007, 12:12
par mostdu95 » 30 Oct 2007, 12:12
bonjour
Quel est le terme maximum dans le developpement de ^{23}) par la formule du binome
par la formule du binome
(indication ; considérer le rapport de deux term:es consécutifs )j'ai beau cherché sans l'indication mais c'est trés compliqué ça fait un long calcul trés compliqué ; car leproblème c'est que je comprend pâs du tout l'indication et l'esprit de l'exercice
donnez moi un coup de pouce s'il vous plait
je vous serait reconnaissant ...allez go !!!!!!
et merci d'avance
-
emdro
- Membre Complexe
- Messages: 2351
- Enregistré le: 11 Avr 2007, 16:37
-
 par emdro » 30 Oct 2007, 12:49
par emdro » 30 Oct 2007, 12:49
Bonjour,
les différents termes sont les

pour k variant entre 0 et 23.
L'énoncé te propose de calculer

...
-
mostdu95
- Membre Relatif
- Messages: 436
- Enregistré le: 09 Sep 2006, 17:36
-
 par mostdu95 » 30 Oct 2007, 13:02
par mostdu95 » 30 Oct 2007, 13:02
ahh ok merci beaucoup je vais essayer et je vous reponderai tout à l'heure ...!!!!
-
mostdu95
- Membre Relatif
- Messages: 436
- Enregistré le: 09 Sep 2006, 17:36
-
 par mostdu95 » 30 Oct 2007, 13:10
par mostdu95 » 30 Oct 2007, 13:10
j'ai :

est ce bien ça ??
-
emdro
- Membre Complexe
- Messages: 2351
- Enregistré le: 11 Avr 2007, 16:37
-
 par emdro » 30 Oct 2007, 13:14
par emdro » 30 Oct 2007, 13:14
Ouh là! Tu t'emportes...
les
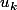
sont juste ce que je t'ai dit, pas la somme!
Si tu préfères,
^{23}=u_0+u_1+...+u_{23})
-
mostdu95
- Membre Relatif
- Messages: 436
- Enregistré le: 09 Sep 2006, 17:36
-
 par mostdu95 » 30 Oct 2007, 13:16
par mostdu95 » 30 Oct 2007, 13:16
mais vous avez dits pour k variant entre 0 et 23 et la formule du binome c'est bien la somme des termes...!!!
-
emdro
- Membre Complexe
- Messages: 2351
- Enregistré le: 11 Avr 2007, 16:37
-
 par emdro » 30 Oct 2007, 13:20
par emdro » 30 Oct 2007, 13:20
mostdu95 a écrit:mais vous avez dits pour k variant entre 0 et 23 et la formule du binome c'est bien la somme des termes...!!!
Même si c'était ce que j'avais dit, il ne faudrait pas me croire aveuglément!
Je n'ai pas dit
la somme des 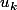
pour k variant de 0 à 23.
j'ai simplement défini
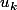
, et j'ai précisé le domaine de validité: pour k variant de 0 à 23.
-
mostdu95
- Membre Relatif
- Messages: 436
- Enregistré le: 09 Sep 2006, 17:36
-
 par mostdu95 » 30 Oct 2007, 13:21
par mostdu95 » 30 Oct 2007, 13:21
ok ce n'est pas grave ...ça sera alors :

-
emdro
- Membre Complexe
- Messages: 2351
- Enregistré le: 11 Avr 2007, 16:37
-
 par emdro » 30 Oct 2007, 13:21
par emdro » 30 Oct 2007, 13:21
Si tu préfères,
^{23}=u_0+u_1+...+u_{23})
Et il s'agit de savoir quel est le plus grand des
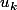
-
emdro
- Membre Complexe
- Messages: 2351
- Enregistré le: 11 Avr 2007, 16:37
-
 par emdro » 30 Oct 2007, 13:22
par emdro » 30 Oct 2007, 13:22
mostdu95 a écrit:ok ça sera alors :

Exact! A toi de simplifier...
-
mostdu95
- Membre Relatif
- Messages: 436
- Enregistré le: 09 Sep 2006, 17:36
-
 par mostdu95 » 30 Oct 2007, 13:30
par mostdu95 » 30 Oct 2007, 13:30
il me reste

c'est mon max de simplification ...!!!
-
emdro
- Membre Complexe
- Messages: 2351
- Enregistré le: 11 Avr 2007, 16:37
-
 par emdro » 30 Oct 2007, 13:32
par emdro » 30 Oct 2007, 13:32
Bof!

et

, tu ne peux pas simplifier?
Et il faut aussi simplifier les coefficients binomiaux en utilisant la formule (avec les factorielles)...
-
mostdu95
- Membre Relatif
- Messages: 436
- Enregistré le: 09 Sep 2006, 17:36
-
 par mostdu95 » 30 Oct 2007, 13:33
par mostdu95 » 30 Oct 2007, 13:33
si j'ai edité avant ..
-
emdro
- Membre Complexe
- Messages: 2351
- Enregistré le: 11 Avr 2007, 16:37
-
 par emdro » 30 Oct 2007, 13:37
par emdro » 30 Oct 2007, 13:37
Pour moi, il nereste qu'un seul 38, et pas 22...
Et il faut aussi simplifier les coefficients binomiaux en utilisant la formule (avec les factorielles)...
-
mostdu95
- Membre Relatif
- Messages: 436
- Enregistré le: 09 Sep 2006, 17:36
-
 par mostdu95 » 30 Oct 2007, 13:41
par mostdu95 » 30 Oct 2007, 13:41
je trouve apres simplification
](23-k)!}{(22-k)!38})
c'est bon ??
-
emdro
- Membre Complexe
- Messages: 2351
- Enregistré le: 11 Avr 2007, 16:37
-
 par emdro » 30 Oct 2007, 13:44
par emdro » 30 Oct 2007, 13:44
Non.
Ne confonds pas numérateur et dénominateur: le k+1 est au dénominateur.
Simplifie (23-k)! et (22-k)!
-
mostdu95
- Membre Relatif
- Messages: 436
- Enregistré le: 09 Sep 2006, 17:36
-
 par mostdu95 » 30 Oct 2007, 13:48
par mostdu95 » 30 Oct 2007, 13:48
ahh d'accord bah ça fait
}{(k+1)38})
donc c'est ce truc la raison de
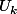
mais comment trouver le plus grand terme ??
......
-
mostdu95
- Membre Relatif
- Messages: 436
- Enregistré le: 09 Sep 2006, 17:36
-
 par mostdu95 » 30 Oct 2007, 13:51
par mostdu95 » 30 Oct 2007, 13:51
ptet il faut trouver la limite de
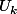
...!!!!!
-
emdro
- Membre Complexe
- Messages: 2351
- Enregistré le: 11 Avr 2007, 16:37
-
 par emdro » 30 Oct 2007, 13:57
par emdro » 30 Oct 2007, 13:57
mostdu95 a écrit:}{(k+1)38})
Oui.
mostdu95 a écrit:mais comment trouver le plus grand terme ??
......
Réfléchir!
la limite de
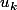
? alors que k est bloqué entre 0 et 23?
Pourquoi as-tu fait le quotient? si ce n'est parce que c'était proposé?
-
mostdu95
- Membre Relatif
- Messages: 436
- Enregistré le: 09 Sep 2006, 17:36
-
 par mostdu95 » 30 Oct 2007, 14:07
par mostdu95 » 30 Oct 2007, 14:07
ah je crois que j'ai trouvé en fait le terme max c'est

qu'on pourra calculé par ce que tout à l'heure on a trouvé la raison de
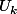
qui est
}{38(k+1)})
je trouve

donc
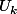
=
{\frac{17(23-k)}{38(k+1)}]^{n})
donc

= y a un poblème par ce que je trouve 0 si je remplace k par 23..!!!
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 28 invités
