Formes alternées !

[barbu23]

Bonjour :
Pouvez vous me traduire mathematiquement ce petit texte que j'ai pas reussi à comprendre :
Soit . Alors, si , soit le determinant de matrice ayant comme vecteurs colonnes. C'est une forme alternée sur .
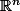
Plus Generalement, si , et on a une suite , on peut definir une forme - alternée en associant à vecteurs le mineur de la matrice ayant obtenu en choisissant les lignes correspondantes à :

Ce que j'ai pas compris est ecrit en gras caractère ! pouvez vous me dessiner une matrice et me montrer dedans ou se situe l mineur decrit çi-dessus !
Merci infiniment !

[Joker62]

Haileau

Bé en fait, en te donnant une suite croissante (i_1, ..., i_r) , tu te donnes un certain nombre de colonne à extraires (tu t'en donnes r) :

Tu prends la colonne n° i_1, tu la place dans ta nouvelle matrice
Tu prends la colonne n° i_2, tu la place à côté.

Et en réitérant jusqu'à i_r, tu obtiendras ta matrice rxr avec laquelle on peut faire le rapprochement décrit plus haut dans ton énoncé ( Valable pour les matrices carrées)

Donc en gros, si t'as une matrice rectangulaire avec plus de colonnes que de lignes, on peut choisir r colonnes celle qui contiennent les v_i, pour se ramener au cas précédent ...

[barbu23]

Merci beaucoup Joker !