Dans mon cours, il est écrit ce qui suit :
Soit
Soient
Puisque
Puisque
avec :
Ma question est :
Je ne comprends pas à quoi est égale
Merci d'avance. :happy3:
P-formes alternées
6 messages
- Page 1 sur 1
p-formes alternées
par barbu23 » 20 Sep 2012, 13:20
Bonjour à tous,
Dans mon cours, il est écrit ce qui suit :
Soit
un 
- espace vectoriel de dimension 
.
Soient $)
, et 
vecteurs 
, que l'on peut écrire dans la base 
sous la forme : 
.
Puisque
est multilinéaire, alors :
 = \alpha \Big( \displaystyle \sum_{i_{1} = 1 }^n v_{1,i_{1}} e_{i_{1}} , ... , \displaystyle \sum_{i_{r} = 1 }^n v_{1,i_{r}} e_{i_{r}} \Big) = \displaystyle \sum_{i_1 , ... , i_r = 1}^n v_{1,i_{1}} ... v_{r,i_{r}} \alpha ( e_{i_{1}} , ... , e_{i_{r}} ) $)
Puisque est alternée, alors :
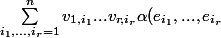 = \displaystyle \sum_{1 \leq i_1 < ... < i_r \leq n} \alpha ( e_{i_{1}} , ... , e_{i_{r}} ) \Big( \displaystyle \sum_{j_{1} , ... , j_{r} \in \{ i_{1} , ... , i_{r} \}} \delta_{j_{1} ... j_{r}}^{i_{1} , ... , i_{r}} v_{1,i_{1}} ... v_{r,i_{r}} \Big) $)
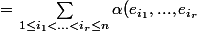 \det ( v_{h,i_{\ell}} )_{h , \ell = 1 , ... , r } = \displaystyle \sum_{1 \leq i_1 < ... < i_r \leq n} \alpha ( e_{i_{1}} , ... , e_{i_{r}} ) ( \varphi_{i_{1}} \wedge ... \wedge \varphi_{i_{r}} ) ( v_1 , ... , v_r ) $)
avec : ( v_1 , ... , v_r ) = \displaystyle \sum_{i_1 , ... , i_r = 1}^{r} \delta_{1,...,r}^{i_{1} , ... , i_{r}} \varphi_{1} ( v_{i_{1}} ) ... \varphi_{r} ( v_{i_{r}} ) = \det ( \varphi_{i} ( v_{j} ) )_{i,j=1 , ... , r } $)
Ma question est :
Je ne comprends pas à quoi est égale ( v_1 , ... , v_r ) $)
dans une matrice 
, quant on fait varier 
dans 
avec 
... Pouvez vous me résumer cette expression dans une matrice pour voir plus clair quant les varient dans ?
Merci d'avance. :happy3:
Dans mon cours, il est écrit ce qui suit :
Soit
Soient
Puisque
Puisque
avec :
Ma question est :
Je ne comprends pas à quoi est égale
Merci d'avance. :happy3:
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 19 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :