Formes bilinéaires-Formes quadratiques-Endomorphismes auto-adjoints

[Diaz]

Bonjour à tous!

Je suis étudiant en 2ème année de Maths.Je suis un nouveau venu sur ce site.Toutefois,je suis déjà très impressionné par ce que je lis ici.
Je suis en train de préparer un concours,qui aura lieu en début avril;pour ce faire,je suis en train de traiter les anciennes épreuves de ce concours.Je compte bien,chaque fois que je rencontrerai un problème dans ma préparation,venir vous le soumettre:Je vous prie,à ces moments-là,d'avoir l'amabilité de m'aider.
Pour l'instant,en traitant l'épreuve d'algèbre de la session 2004 de ce concours,j'ai rencontré des problèmes au niveau des questions lll et lV;j'ai alors consulté le corrigé de l'épreuve,mais,hélas,même lui je ne l'ai pas compris(peut-être parce que j'ignore certains théorèmes).
Je vous présente alors l'énoncé des questions lll et lV,afin,s'il vous plaît,que vous m'aidiez (N'oubliez surtout pas,je vous en prie,d'énoncer les théorèmes ou propositions utilisés;en effet,il est possible que si je n'ai pas compris,c'est parce que j'ignore les théorèmes qu'il faut utiliser).
Voici l'énoncé:

lll.
Soit E un espace vectoriel de dimension 2,muni d'un produit scalaire,que l'on notera,pour 2 vecteurs u,v appartenant à E,[u,v].Soit f un endomorphisme aoto-adjoint de E.On définit alors une forme quadratique q de E vers R,par q(u)=[f(u),u].

1.Montrer que q change de signe sur E(i.e qu'il existe u;v appartenant à E tels que q(u)q(v) est strictement inférieur à 0) ssi det f (det f=déterminant de f)est strictement inférieur à 0.
2.Montrer que q ne change pas de signe ssi Z(q)=x appartenant à E /q(x)=o est un sous-espace vectoriel de E.

lV.
On considère ici l'espace F=l'ensemble des matrices A telles que A est une matrice carrée d'ordre 2 à coefficients réels et Tr(A)=0,Tr(A) désignant la trace de A.

1.Montrer que F est un sous-espace vectoriel de l'ensemble des matrices d'ordre 2,à coefficients réels ;vérifier que:
1 0 0 1 0 0
e1= e2= e3= en est une base.
0 -1 0 0 1 0

2.Montrer que si on définit [A,B]=Tr((tA)B)(tA désigne la transposée de A), alors l'ensemble des matrices d'ordre 2,à coeficients réels,muni de[.,.]est un espace vectoriel euclidien.

3.Si A est une matrice carrée d'ordre 2,à coefficients réels,exprimer le projeté orthogonal de A sur F.

4.Trouver une base orthonormée (f1,f2,f3) de (F,[.,.]),en orthonormalisant la base (e1,e2,e3).

5.L'application qui,à A,associe det A,est une forme quadratique sur F;montrer qu'il existe un unique endomorphisme autoadjoint u de E tel que:
pour tout A appartenant à E,det A=[u(A),A].

6.Déterminer la matrice de u dans la base (f1,f2,f3),les valeurs propres de u,et la signature de la forme quadratique qui,à A,associe det A.

MERCI D'AVANCE!
MERCI D'AVANCE!

[El_Gato]

Salut,

Commençons par le début.

III
1- Puisque f est auto-adjoint, il a toutes ses valeurs propres réelles et il est diagonalisable dans une base orthonormée pour le produit scalaire, base que l'on note . Dans cette base, la matrice de f est de forme:

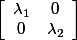
et det(f) = .

Soit u un vecteur quelconque de coordonnées dans 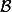. On a:
.
Donc si le déterminant de f est < 0,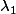 et 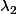sont de signes contraires, et, puisque 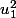et 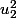sont positifs, on trouve immédiatement deux u et v qui sont tels que q(u)q(v) < 0.

Reciproquement, s'il existe deux tels u et v, en remontant le raisonnement ci-dessus on trouve que les valeurs propres de f sont nécessairement de signes contraires et donc que son déterminant est < 0.

[El_Gato]

III
2- Soit toujours la base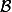 orthonormée pour f définie ci-dessus. Pour un vecteur x de coordonnées dans cette base, on a donc:
.
On fait une classification en fonction du déterminant de f. Comme q ne change pas de signe, det(f).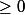
1er cas, det(f) non nul. Dans ce cas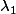 et 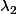sont tous deux strictement positifs ou tous deux strictement négatifs et Z(q) = {0}.
2ième cas det(f) = 0: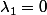 , 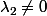. Z(q) est l'ensemble des x tels que 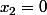: c'est un s.e.v de dim 1.
3ième cas det(f) = 0: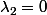 , 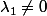. Z(q) est l'ensemble des x tels que 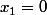: c'est un s.e.v de dim 1.
CQFD.

En conclusion, pour résoudre cette question III, il suffit de se placer dans une base orthonormée adaptée à f.

[El_Gato]

lV.
On considère ici l'espace F=A/A est une matrice carrée d'ordre 2 à coefficients réels et Tr(A)=0,Tr(A) désignant la trace de A.

Je ne comprend pas la notation. C'est quoi F ?

[Diaz]

Je ne comprend pas la notation. C'est quoi F ?

Merci beaucoup El_Gato!Je te pardon pour l'énoncé;je ne m'étais pas rendu compte de l'erreur:je l'ai modifié,à présent.J'attends donc la réponse à la question IV.
Merci encore!

[Diaz]

Toujours dans le cadre de la préparation de mon concours,j'aimerais savoir si on peut affirmer les assertions suivantes:
1-Pour parler d'espace vectoriel sur un corps K,il faut au préalable que le corps K soit commutatif.
2-Si E est un espace vectoriel sur un corps K,alors E est un espace vectoriel sur tout sous-corps de K.
Merci d'avance.
P.S:N'oubliez pas de m'envoyer la réponse de la question IV,s'il vous plaît.

[El_Gato]

Ah et pour le III-2 j'ai oublié un cas: det(f) = 0 et les deux valeurs propres nulles. Dans ce cas Z(q) = l'espace E entier, de dim 2.

[Diaz]

Ah et pour le III-2 j'ai oublié un cas: det(f) = 0 et les deux valeurs propres nulles. Dans ce cas Z(q) = l'espace E entier, de dim 2.

S'il te plaît,n'oublie pas de m'envoyer la réponse de la question IV.
Merci!