Forme tri-linéaire

[Alphonso_de_las_vegas]

Bonjour,

On parle souvent de forme linéaire ou bilinéaire (produit scalire) ou encore du déterminant ! Mais alors les formes tri-linéaire ?

[Joker62]

Hello,

C'est quoi la question ?

[Alphonso_de_las_vegas]

Salut de Lille,

la question c'est pourquoi les formes bilinaire sont étudiés et non les formes 3-linéaire ?

[Joker62]

Re de Lille :)

Les formes bilinéaires donnent parfois des produits scalaires, des formes quadratiques.
Les formes tri-linéaires non :D

[Alphonso_de_las_vegas]

Re de Lille

Les formes bilinéaires donnent parfois des produits scalaires, des formes quadratiques.
Les formes tri-linéaires non

Oui mais pourquoi ?

[Joker62]

http://pmb.univ-fcomte.fr/2009/Nyssen.pdf

[Ben314]

Salut,
Bon, déjà, il ne faut pas dire que l'on ne manipule jamais de formes trilinéaires : le déterminant sur un e.v. de dim 3 est une forme trilinéaire.
Aprés, c'est vrai que l'on manipule ça moins souvent que les formes bilinéaires, mais ça vient du fait que sur un e.v. de dim fini, pour connaitre une forme n-linéaire, il suffit de la connaitre sur les n-uplets de vecteurs faisant parti d'une base.
Pour une forme linéaire, il suffit donc de connaitre les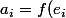 qui forment donc un vecteur (indexé avec )
Pour une forme bilinéaire, il suffit donc de connaitre les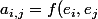 qui forment donc une matrice carrée (indexé avec et ) et une bonne partie de la théorie raproche cette matrice de celle d'une application linéaire de E dans E (ou plus précisément de E dans le dual de E).
Pour une forme trilinéaire, il suffit donc de connaitre les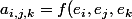 qui forment donc... une espèce de matrice "cubique" (indexé avec et ) et là, on sait pas trop à comment rapprocher ce type d'objet d'une structure simple...