Formalisme d'événements probabilités

[MoonX]

Bonjour

On considère un lancer de pile ou face infini.
Je cherche à montrer le calcul des probabilités suivantes :

P(il sort une infinité de pile)=1
P(il sort des séquences arbitrairement longue de P consécutifs) = 1
P( P est majoritaire pour les n premiers lancers) = 0

De plus, j'ai aussi l'expression d'une loi sur laquelle je bloque :
Loi de s'il est sorti autant de P que de F pour la première fois au rang 2n, si les nombres de P et F sont constamment différents.

Sauf que je ne sait comment exprimer ces événements de manière à calculer simplement.
Plus généralement, pouvez vous m'indiquer la démarche à suivre pour exprimer ce genre d'événement ?

Je vous remercie par avance !

[mathelot]

Bonjour

On considère un lancer de pile ou face infini.
Je cherche à montrer le calcul des probabilités suivantes :

P(il sort une infinité de pile)=1

*
l'évènement complémentaire est "il ne sort qu'un nombre fini de piles,
dc à partir d'un certain rang , il ne sort plus que des faces.

[Skullkid]

Bonjour, j'ai pas essayé de faire les calculs mais globalement, définir la loi uniforme sur une infinité de pile ou face, c'est-à-dire sur l'espace , c'est faisable mais plutôt pénible à manipuler en pratique. Du coup il vaudrait sans doute mieux que tu considères les probas qui t'intéressent pour N lancers (là la loi uniforme est simple : chaque suite finie à une proba de sortir), puis que tu fasses tendre N vers l'infini.

[beagle]

..............................................................

[Ben314]

Salut,

Bonjour, j'ai pas essayé de faire les calculs mais globalement, définir la loi uniforme sur une infinité de pile ou face, c'est-à-dire sur l'espace , c'est faisable mais plutôt pénible à manipuler en pratique. Du coup il vaudrait sans doute mieux que tu considères les probas qui t'intéressent pour N lancers (là la loi uniforme est simple : chaque suite finie à une proba de sortir), puis que tu fasses tendre N vers l'infini.

Sauf que dans pas mal de cas, de se limiter à des trucs finis, ça ne permet pas de répondre bien proprement à la question posé.
Par exemple, pour la question (1) "proba d'avoir une infinité de Pile", si on regarde ça en terme fini, on peut dire que, pour k fixé, la proba d'avoir moins de k fois Pile sur les n premiers lancés tend vers 0 lorsque n tend vers l'infini. Donc on peut "déduire naïvement" que la proba d'avoir moins de k fois Pile sur une infinité de lancés est nulle. Sauf que pour conclure que la proba de ne tirer qu'un nombre fini de fois Pile (sur une infinité de lancés) est nulle, il faut un (très lourd) argument théorique, à savoir la dénombrable additivité de la mesure.
Et perso., ça me semble plus que gonflé de rester à un niveau "naïf" (i.e. de juste regarder les proba sur N tirages puis de faire tendre N->oo) et d'affirmer qu'il "est évident" que c'est dénombrement additif...

Bref, je pense pas qu'on puisse s'en sortir bien proprement (*) sans connaitre un minimum quelle est la tribu qu'on considère sur l'espace {P,F}^N ainsi que la mesure qu'on prend sur cette tribu.

(*) Évidement, on peut "donner des idées de la preuve", mais à mon avis, surement pas une "vrai" preuve.

[beagle]

a un niveau naif, on se dit que lorsque les pile seront épuisés, alors face devra tout assurer, mais on se doute que cela va épuiser face, et que comme il a une proba de face limité non nulle également,
finalement au bout d'un moment il n' ya plus ni pile , ni face.

Bon, Ok je sors!

Ps: une dernière
si la proba de pile fini est non nulle, la proba de face fini non nulle bien sur,
alors proba des évènements pile fini et face fini ne peuvent ètre indépendants sinon, c'est proba qu'il ne sorte rien ?

[beagle]

ceci n'est pas du formalisme.
Soit il ya un nombre fini de pile et ensuite on re retrouve que des face à l'infini
cela signifie qu'il existe des séries où face peut sortir à l'infini tout seul.
Soit l'infini de face se trouve entre deux sorties de pile, et là on ne voit pas quel numéro ordinal donner à l'arrivée du "second" pile, bref le dénombrable ne marche plus.Peut-ètre que cela rejoint le " à savoir la dénombrable additivité de la mesure" de Ben314 pour faire du formalisme.

[MoonX]

Merci à tous pour vos réponses.
Le cas du pile ou face est admis en prépa, c'est plutôt pour faire des exercices de calcul, "on s'en fiche un peu de l'univers ou de la tribu" m'a-t-on dit...

Alors, si je dénote les événements par A, B et C, on a déjà :
(A = il sort une infinité de pile ; B = il sort des séquences arbitrairement longue de P consécutifs ; C = P est majoritaire pour les n premiers lancers)

P(A) = 1 - P(
Or, P( (par indépendance des lancers, la probabilité est un "produit infini nul")
D'où P(A) = 1

Je ne vois toujours pas pour les événements suivants, mais je suppose que l'utilisation de variable aléatoire doit rendre cela plus facile ?

Je me suis permis de rajouter le calcul d'une loi à mon message d'origine, ça reste dans le cadre des piles ou faces infini et je ne souhaite pas surcharger le forum avec mes pile ou face

[Elias]

P( il sort des séquences arbitrairement longues de piles)=1.

Je note

Il faut montrer que pour tout entier k, l'ensemble des suite contenant la séquence (avec k fois 1) est de mesure 1 pour la probabilité P.

On peut découper cet ensemble en :
-les suites pour lesquelles le premier rang à partir duquel apparaît est 1;
-les suites pour lesquelles le premier rang à partir duquel apparaît est 2;
-les suites pour lesquelles le premier rang à partir duquel apparaît est 3;

etc...

On créé des sous ensembles deux à deux disjoints dont on peut calculer la probabilité (i.e. la mesure pour P)

On somme le tout et on doit obtenir une série géométrique de somme 1.

[MoonX]

Merci pour votre réponse.

Si on note A_{k,n} = "la première fois qu'une suite de longueur k apparaît est au rang n", alors on peut calculer pour n<k. Mais par contre, j'arrive pas à calculer pour n>=k...

Je sais pas si c'est la meilleure idée, mais je vois pas comment faire sinon...

Du coup je ne vois pas non plus quel ensemble deux à deux disjoints je peux faire ?

[Ben314]

Pour celui là :

P(il sort des séquences arbitrairement longue de P consécutifs) = 1

c'est tellement évident que c'est pas la peine de s'emmerder dans la preuve :
Pour k fixé, la proba que les k premiers ne soient pas tout des P est 1-1/2^k. La proba que les k suivant ne soient pas tous de P est aussi 1-1/2^k et c'est évidement indépendant des k premiers, etc...
De façon générale, si on coupe les n.k premiers tirages en n "tranches" de k, la proba qu'aucune de ces tranche ne soit entièrement constituée de P est de (1-1/2^k)^n. Et clairement, ça tend vers 0 lorsque n->oo donc la proba de ne jamais avoir k fois P de suite quand on coupe "k par k" est nulle.
Et bien sûr, ça implique que la proba de ne jamais avoir k fois P de suite (situés n'importe où) est elle aussi nulle.

Reste le point délicat (qu'on ne peut pas éviter...) consistant à dire que la proba de ne pas avoir de séquence arbitrairement longue est une réunion dénombrable d'évènement de proba nulle donc est de proba nulle.

En fait, LE truc intéressant (à mon sens) dans tes proba, c'est la troisième où je sais pas si on peut s'en sortir (comme ici) en raisonnant "avec des gros sabots" et plus précisément si on peut s'en sortir sans utiliser le "principe de symétrie" qui permet de calculer la proba explicite de repasser à 0 lors d'une marche aléatoire dans Z de longueur N.

[MoonX]

D'accord, merci je comprend mieux.

Si vous parlez de P(pour tout n, P est majoritaire pour les n premiers lancers) = 0, j'ai peut-être une petite idée. En utilisant la formule des probas composés, on trouve à la main et on montre facilement par récurrence que la proba de l'événement A_n "Il a une majorité de pile pour les n premiers lancers" vérifie :
P(A_2n) = 1/2^(n+1)
P(A_{2n+1}) = 1/2^(n+1)
(En tout cas, il me semble)

Ensuite, la suite des A_n est décroissante au sens de l'inclusion. Donc, d'après un théorème de décroissance que j'ai dans le cours, la proba de l'intersection pour n dans N (i.e. notre événement) est égale à la limite lorsque n tend vers l'infini de P(A_n), qui vaut bien sûr 0.

Est-ce correct selon vous ?

Ensuite, pour ma variable aléatoire je n'ai aucune idée de comment procéder...

[Ben314]

J'ai plus que de gros doute concernant le fait que :

...la proba de l'événement A_n "Il a une majorité de pile pour les n premiers lancers" vérifie :
P(A_2n) = 1/2^(n+1)
P(A_{2n+1}) = 1/2^(n+1)

Vu que si on ne considère pas les cas où il y a exactement le même nombre de P que de F (cas dont la proba tend vers 0 lorsque n->oo) alors parmi les autres, il y en a évidement la moitié où c'est les P qui sont majoritaires.
Ou alors, c'est que ton évènement An, c'est que, pour tout k<=n, le segment initial composé des k premiers lancés est majoritairement composé de P, mais dans ce cas, déjà il faudrait préciser le sens de "majoritaire" (strict ou large) et en plus, ça m'étonnerais fort que la proba soit aussi simple que ton p(A_2n)=1/2^(n+1).

[MoonX]

Je vais expliciter le raisonnement que j'ai tenu.
J'ai considéré que majoritaire était au sens strict.

Je note : "P est majoritaire pour les n premiers lancers".

Ensuite.
- P(A_1) = 1/2 bien évidemment.
- P(A_2) = 1/2^2, car on doit tirer un pile au début, puis encore un pile sinon on a plus une majorité de P au sens strict.
- P(A_3) = 1/2^2 : Si au rang 2 on avait une majorité de P, on en avait 2 sur 2. Donc là on peut tirer n'importe quoi.

J'ai alors montré le résultat par récurrence :
Initialisation : fait
Itération : soit n dans N. Supposons le résultat vrai au rang n.
(qui est nul car si l'événement n'est pas vérifié au rang n, il ne peut l'être au rang n+1).
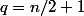
- Si n est pair : on a k\geq n/2 + 1 Piles au rang n. Or, pour avoir une majorité au rang n+1, il faut au moins piles, ce qui est vérifié. Donc
- Si n est impair : écrivons
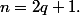
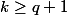
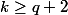
On a Piles au rang n. Donc, pour avoir une majorité au rang n+1, il faut , donc . Il faut donc tirer un pile, d'où
(Ici, je suis pas sûr de mon raisonnement finalement...)

Si tout est juste, j'ai démontré ce que j'ai dis plus haut. L'est-ce ?
(Après réflexion, le passage "n impair" n'est peut-être pas juste).

[Pseuda]

Bonsoir,

Ouh là. Si on considère une majorité stricte, P(A3) est la probabilité d'avoir 2 piles et 1 face parmi 3 lancers ou d'avoir 3 piles. Loi binomiale : 3/8 +1/8 = 1/2.

Pour la suite, c'est (1-probabilité d'avoir le même nombre de piles que de faces)/2 si n est pair, et si n est impair, c'est 1/2. Enfin, dans le sens où on comprend une majorité stricte "au bout" du nième lancer.

[Ben314]

J'ai pas trop regardé la suite (je regarde), mais vu le début de sa prose, le An qu'il considère, ce n'est pas (contrairement à ce qu'il dit) "la proba que les P soient majoritaires sur les n premier lancés", mais (comme je le soupçonnais dans le précédent post.) "la proba que les P soient majoritaires dans tout les segment initiaux des n premiers tirages".
Par exemple, avec le tirage PFP les P sont effectivement majoritaires sur les 3 tirages, mais il ne le sont pas (strictement) sur le segment initial composé des 2 premiers, à savoir PF. Et, toujours avec 3 tirages, les cas où non seulement les P sont (strictement) majoritaire sur les 3 tirages, mais où il le sont aussi sur les segment initiaux sont PPP et PPF ce qui donne bien le 2/8=1/4 annoncé.

EDIT (j'ai lu la suite) :

- Si n est impair : écrivons
On a Piles au rang n. Donc, pour avoir une majorité au rang n+1, il faut , donc . Il faut donc tirer un pile, d'où
(Ici, je suis pas sûr de mon raisonnement finalement...)

Effectivement : là, c'est très clairement faux : si pour le moment (au rang n), tu as exactement un et un seul Pile d'avance sur les Faces (c'est en dire en reprenant tes notation si k est égal à q+1), alors effectivement, il faut forcément tirer un Pile le coup suivant pour que les Piles restent (strictement) majoritaires. Donc là, ça fait bien une proba de 1/2. Mais bien évidement si tu as strictement plus d'un Pile d'avance (c'est en dire si k est strictement plus grand que q+1) alors tu peut tirer n'importe quoi, le coup suivant le nombre de Pile restera majoritaire.

Par exemple, si n=3, pour le moment, tu as soit PPF et effectivement il faut obligatoirement un P pour que ça marche, soit tu as PPP et dans ce cas, ben tu peut tirer un P ou un F et dans les deux cas c'est O.K. vu que tu avait des P "d'avance".
Bref, P(A3)=2/8 (PPF et PPP) qui est bien égal au 1/2^2 que tu annonce, mais par contre P(A4)=3/16 (PPFP ; PPPF et PPPP)

[MoonX]

Merci pour vos réponses
Du coup j'ai du mal à comprendre deux choses :

1) Comment doit-on comprendre "majorité de Pile pour leS n premierS lancerS" ? (je mets le s en majuscule pour vous montrez ce qui me fait penser ce qui semble être faux).
2) Cependant, si je choisis l'événement A_n comme je l'ai défini, ça devrait toujours marcher pour montrer ce que je veux puisque c'est pour tout n ? (Si j'arrive et s'il est possible de calculer la probabilité bien sûr). Conditionner le tirage pair en fonction des du nombre de pile de tout les tirages impairs devrait alors fonctionner puisque ces tirages sont censés être "libre de choix" ?

Mais même si ma méthode venait à aboutir, je la trouve vraiment compliquée (dans le sens, tirée par les cheveux)... auriez vous une méthode plus élégante ?

[Ben314]

Si je me suis pas gouré, parmi les tirages possible de pièces, il y en a (coeff. binomial) où les Piles sont strictement majoritaires sur tout les segment initiaux (non vide) du tirage.