Fonction intégrable sur une sphère

[Rhaegar]

Bonjour,

Pour la résolution d'un exercice, je dois montrer que la fonction définie par est intégrable sur la sphère . Le réel est la première composante de dans . Autrement dit, on doit montrer que . La mesure en question est la mesure de Lebesgue normalisée sur la sphère ().

Je pense qu'il faut utiliser une manip pour se ramener sur en utilisant les coordonnées hypersphériques mais ça me paraît bien trop compliqué et de plus je ne sais pas les utiliser. Je ne suis pas du tout calé sur les variétés différentielles. Je me demandais s'il n'y avait pas un autre moyen, plus simple, de le montrer.

Bien à vous,
Rhaegar

[GaBuZoMeu]

Bonsoir,

Ton histoire me semble très louche. Considérons par exemple le cas de la sphère de dimension 2 dans . Il est bien connu que l'aire (normalisée comme tu dis) de la portion de sphère comprise entre deux plans verticaux distants de coupant la sphère est .
Tu voudrais donc avoir une intégrale . Hum hum ...

Vérifie ton énoncé.

[Rhaegar]

Bonsoir GaBuZoMeu,

Je ne connaissais pas ce fait sur la sphère. Est-ce qu'il se généralise en dimension quelconque pour une portion de l'hypersphère comprise entre deux hyperplan ?

J'avoue ne pas vraiment comprendre comment vous faite pour ramener le calcul à cette intégrale 1d. Pourriez-vous détaillé s'il vous plaît ?

[GaBuZoMeu]

C'est tout bête, on intègre sur les tranches à constant. C'est à peu près expliqué là : http://villemin.gerard.free.fr/GeomLAV/Sphere.htm
La projection cylindrique de la sphère sur le cylindre qui l'enveloppe préserve l'aire (voir projection de Lambert en cartographie).
Tel que, c'est uniquement pour la sphère de dimension 2, mais ça montre que ton histoire ne tient pas. D'où la sors-tu ? J'ai l'impression que tu t'es fourvoyé dans la résolution de ton exercice, peux-tu nous en dire plus ?

[Rhaegar]

J'ai du mal à comprendre certain passage de la démonstration sur le site de villemin. ça n'a pas l'air très rigoureux (même si c'est juste). ça doit se passer différemment si on intègre une fonction. J'avoue que si la fonction n'est pas intégrable, je ne vois pas comment résoudre mon problème.

Voici plus de détail sur mon problème :
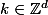
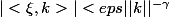
non nulle. R(eps,k) est l'ensemble des vecteurs sur la sphère de dimension d-1 vérifiant . Il faut montrer qu'il existe une constante C>0 telle que pour tout k et tout eps dans ]0,1[, on ait
.

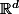
Mon idée est la suivante : je pose m = k/||k||. Ensuite, quitte à faire une isométrie de l'espace, je peux supposer que m est le premier vecteur de la base canonique de . Ainsi,.
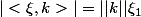
Je calcul ensuite la mesure de R(k,eps) avec une intégrale :
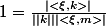
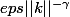
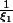
. Or . Je majore la partie du haut par car . La partie du bas devient . Si je montre que la fonction est intégrable sur la sphère, j'ai ma constante C et l'inégalité est prouvée.

[GaBuZoMeu]

Ton calcul de l'aire de ne va pas. C'est l'"aire" de la tranche de sphère entre et . La majoration de cette aire de la forme demandée ne pose pas de gros problème. Remarque : pour , cette aire vaut exactement .

[Rhaegar]

Je cherchais à majorer l'aire de la tranche de sphère, en utilisant le propriété sur le produit scalaire. Mon idée me semblait la plus naturelle car j'utilise la majoration sur le produit scalaire et aucun arguments géométriques (c'est un cours d'analyse normalement). Vous dîtes que la majoration de l'aire ne pose pas de gros problème mais elle m'en pose un de toute évidence. Je comprends votre remarque pour d=3 mais si je veux le montrer pour une dimension quelconque, ce fait doit rester vrai et je dois le démontrer ce qui fait appelle à des compétences de géométries que je n'ai malheureusement pas.

[GaBuZoMeu]

Tu vois bien que ta majoration ne fonctionne pas puisqu'elle conduit à une intégrale divergente.
Calculer le volume de la tranche de sphère ne me semble pas requérir des connaissances géométriques extravagantes. Quand on coupe par l'hyperplan de première coordonnée, on obtient un parallèle de la sphère qui est une -sphère de rayon . Son -volume est donc le volume de la sphère unité multiplié par . Pour obtenir le -volume d'une tranche infinitésimale de largeur , on multiplie le -volume du parallèle par l'élément de longueur du méridien qui est . On a donc à intégrer, entre les bornes pour , fois le -volume de la -sphère unité ; ça se majore très facilement pour .

[Rhaegar]

Effectivement, j'avais également pensé à intégrer comme vous le détaillez mais c'est très confus dans ma tête. J'avoue avoir du mal avec ces histoires d'éléments de longueur/aire/volume, de ce genre de changement de variables. J'ai également une mauvaise intuition sur le fait que la surface d'une sphère est égale à la surface du cylindre qui la contient.

Je crois comprendre votre raisonnement et je vais pouvoir résoudre mon problème.

Merci beaucoup pour votre aide !

[GaBuZoMeu]

Avec plaisir.