Fonction hyperbole particulière

[egtls2021]

Bonjour à tous, j'ai besoin de votre aide pour cet exercice que je ne comprends pas :

Montrer que Y = (AX)/(B + X) = (Ymax X)/(X0,5 + X)

Avec Ymax définie comme étant la valeur limite de Y lorsque X tend vers l'infini (+∞)
Et X0.5 , définie comme étant la valeur de X pour laquelle Y est égale à 50% de la valeur maximale de Y
soit Y = Ymax/2.

C'est la première fois que j'utilise le site donc je ne suis pas très à l'aise pour écrire les formules, j'espère que c'est assez compréhensible ! (j'ai mit le sujet en pièce jointe normalement, enfin j'espère)

[egtls2021]

Excusez moi j'ai oublié, l'énoncé dit "Soit la fonction hyperbolique particulière, définie par les paramètres A et B. "

[Pisigma]

Bonjour,

je crois qui manque des parenthèses dans ton énoncé

[egtls2021]

Salut ! Je viens de le modifier, tu penses pouvoir m'aider ?

[Pisigma]

c'est Y = (AX)/(B + X) = (Ymax X)/(X0,5 + X)?

si c'est correct, tu peux calculer Ymax et X0,5

[egtls2021]

La formule initiale est Y = (AX)/(B + X) mais on me demande de montrer que Y = (AX)/(B + X) = (Ymax X)/(X0,5 + X)

[Pisigma]

donc tu calculer Ymax et X0,5

[egtls2021]

Je ne sais pas comment faire, je n'ai aucune valeur

[Pisigma]

Avec Ymax définie comme étant la valeur limite de Y lorsque X tend vers l'infini (+∞)

ou si tu préfères

[egtls2021]

avec ça j'ai répondu à la question ?

[Pisigma]

c'est pas sympa de demander une réponse sur un autre forum.
Je te laisse!

[egtls2021]

Tous les astres sont contre moi aujourd'hui on dirait, je cherche simplement de l'aide sur cet exercice depuis 4h mais je ne comprends toujours pas, j'essaye simplement d'intégrer des notions et on me blâme pour cela, sincèrement ça démoralise, tant pis bonne soirée à toi malgré tout...

[mathelot]

Bonsoir,

est solution de l'équation d'inconnue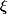



calcule (faire un produit en croix ?)

[egtls2021]

Merci de votre réponse, je vais essayer ça sur le champs !

[Pisigma]

Bonjour mathelot,

c'est "gentil" de répondre à ceux qui postent partout, mais personnellement, à partir du moment où je donne des pistes, je trouve la façon de faire du "posteur" assez irrespectueuse.

Mais, bon, chacun sa façon de voir...

Bonne journée

Pisigma

[Black Jack]

Bonjour,

Y = (AX)/(B + X)

Ymax = lim(X-->+oo) Y = lim(X-->+oo) [(AX)/(B + X)] = A
*****
La valeur de X si (AX)/(B + X) = Ymax (donc = A/2) ... est X0,5

On a donc : (A.X0,5)/(B + X0,5) = A/2

relation de laquelle on tire X0,5 = ...
*****
Et en remplaçant Ymax et X0,5 par ce qui a été trouvé ci dessus dans (Ymax X)/(X0,5 + X), on arrive à démontrer ce qui a été demandé.