Bonjour,
Est-ce que le fait qu'une fonction soit continue implique que les dérivées partielles de la fonction existent?
(dans Rn)
Merci!
Fonction continue et dérivées partielles
2 messages
- Page 1 sur 1
Re: fonction continue et dérivées partielles
par mathelot » 17 Juin 2018, 17:09
non,
soit=x 1_{\mathbb{Q}}(x)+y 1_{\mathbb{Q}}(y))
où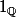
est la fonction indicatrice des rationnels
=1)
si x est rationnel, 0 sinon.
=0)
-f(0;0)}{x}=1_{\mathbb{Q}}(x))
n'a pas de limite quand x tend vers zéro
-f(0;0)}{y}=1_{\mathbb{Q}}(y))
n'a pas de limite quand y tend vers zéro
or
-f(0;0)| \leq |x|+|y|)
f est continue en (0;0)
soit
où
or
f est continue en (0;0)
2 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 28 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :