Fonction constante
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
elvis77
- Membre Relatif
- Messages: 156
- Enregistré le: 05 Fév 2008, 19:52
-
 par elvis77 » 02 Fév 2014, 17:39
par elvis77 » 02 Fév 2014, 17:39
Bonjour,
Une question me gène :
J'ai :
=0)
pour un certain

qui appartient à un ouvert.
Alors la fonction est localement constante (i.e égale à 0) sur un voisinage de

Est ce bien vrai ? comment m'en persuader et/ou le démontrer ?
Merci
Cordialement.
-
Imod
- Habitué(e)
- Messages: 6484
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 02 Fév 2014, 18:12
par Imod » 02 Fév 2014, 18:12
C'est bien sûr faux , prendre par exemple f(x)=x² sur R , f(0)=0 et après ?
Imod
-
elvis77
- Membre Relatif
- Messages: 156
- Enregistré le: 05 Fév 2008, 19:52
-
 par elvis77 » 02 Fév 2014, 18:39
par elvis77 » 02 Fév 2014, 18:39
merci pour votre réponse.
Même si f est à valeurs entières ?
-
Imod
- Habitué(e)
- Messages: 6484
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 02 Fév 2014, 19:15
par Imod » 02 Fév 2014, 19:15
La question n'est pas claire , f est définie de R dans N ? Continue ?
Imod
-
elvis77
- Membre Relatif
- Messages: 156
- Enregistré le: 05 Fév 2008, 19:52
-
 par elvis77 » 02 Fév 2014, 19:19
par elvis77 » 02 Fév 2014, 19:19
Imod a écrit:La question n'est pas claire , f est définie de R dans N ? Continue ?
Imod
oui, f est définie de

dans

et à un complexe elle associe le nombre de valeurs critiques d'un polynome.
-
Rha
- Membre Naturel
- Messages: 51
- Enregistré le: 21 Oct 2013, 22:35
-
 par Rha » 02 Fév 2014, 22:15
par Rha » 02 Fév 2014, 22:15
elvis77 a écrit:oui, f est définie de

dans

et à un complexe elle associe le nombre de valeurs critiques d'un polynome.
Si l'application est effectivement continue, l'image réciproque de

par cette application est un ouvert de

, car

est un ouvert de

.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 03 Fév 2014, 11:16
par Ben314 » 03 Fév 2014, 11:16
elvis77 a écrit:oui, f est définie de

dans

et à un complexe elle associe le nombre de valeurs critiques d'un polynome.
C'est quoi que tu appelle un "point critique" pour un polynôme ?
C'est quoi le lien entre le complexe de départ (celui de l'application de C dans N) et le polynôme ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
elvis77
- Membre Relatif
- Messages: 156
- Enregistré le: 05 Fév 2008, 19:52
-
 par elvis77 » 03 Fév 2014, 11:33
par elvis77 » 03 Fév 2014, 11:33
Ben314 a écrit:C'est quoi que tu appelle un "point critique" pour un polynôme ?
C'est quoi le lien entre le complexe de départ (celui de l'application de C dans N) et le polynôme ?
Mon problème était plus profond que ça : je voulais montrer que l'application :
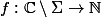
telle que :
=card(P^{-1}({\alpha})))
où
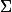
est l'ensemble des valeurs (et non des points) critiques d'un polynome
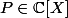
est localement constante. Mais je pense m'en être sortie avec des suites et en raisonnant par l'absurde.
Merci.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 03 Fév 2014, 12:00
par Ben314 » 03 Fév 2014, 12:00
elvis77 a écrit:...est l'ensemble des valeurs (et non des points) critiques d'un polynome
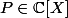
...
C'est quoi pour toi un "point critique" pour un polynôme de
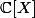
?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
elvis77
- Membre Relatif
- Messages: 156
- Enregistré le: 05 Fév 2008, 19:52
-
 par elvis77 » 03 Fév 2014, 12:22
par elvis77 » 03 Fév 2014, 12:22
Ben314 a écrit:C'est quoi pour toi un "point critique" pour un polynôme de
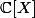
?
point critique =
=0)
valeur critique = la valeur que donne le polynome pris au point critique

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 03 Fév 2014, 12:37
par Ben314 » 03 Fév 2014, 12:37
elvis77 a écrit:point critique =
=0)
valeur critique = la valeur que donne le polynome pris au point critique
Sauf erreur, dans ce cas, par construction, ta fonction f est constante égale au degré

du polynôme :
Pour que
)
soit distinct de

, il faut (et il suffit) que le polynôme
=P(X)-\alpha)
admette au moins une racine au moins double, c'est à dire qu'il existe
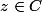
tel que
=Q'_\alpha(z)=0)
ce qui signifie que
=\alpha)
et
=0)
c'est à dire que

est ce que tu appelle une "valeur critique"...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
elvis77
- Membre Relatif
- Messages: 156
- Enregistré le: 05 Fév 2008, 19:52
-
 par elvis77 » 03 Fév 2014, 12:48
par elvis77 » 03 Fév 2014, 12:48
Etrange... par la suite je montre que ma fonction

est constante (localement donc partout) égale à 0 (sous les hypothèses, 0 n'appartient pas à
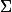
et P n'a pas de racines.)

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 03 Fév 2014, 14:51
par Ben314 » 03 Fév 2014, 14:51
Le fait que
=card(P^{-1}({\alpha})))
puisse être nul ne serait-ce qu'en un seul point contrdirait le fait que
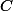
est algébriquement clos...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 03 Fév 2014, 14:52
par Ben314 » 03 Fév 2014, 14:52
elvis77 a écrit:...et P n'a pas de racines.)
Heuuuuuu, tu sait que
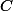
est algébriquement clos ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Ezra
- Membre Naturel
- Messages: 95
- Enregistré le: 10 Déc 2013, 16:52
-
 par Ezra » 03 Fév 2014, 15:32
par Ezra » 03 Fév 2014, 15:32
Ben314 a écrit:Heuuuuuu, tu sait que
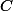
est algébriquement clos ?
Le polynôme

ne peut pas ne pas avoir de racine. C'est le théorème de d'Alembert-Gauss :
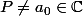
, scindé, a au moins une racine dans

et le nombre de racines de

dans

est égal à :
)
...
-
elvis77
- Membre Relatif
- Messages: 156
- Enregistré le: 05 Fév 2008, 19:52
-
 par elvis77 » 03 Fév 2014, 21:03
par elvis77 » 03 Fév 2014, 21:03
le but étant justement de démontrer le théorème de d'Alembert Gauss...
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 94 invités
dans
et à un complexe elle associe le nombre de valeurs critiques d'un polynome.
=0)