Intégration, fonction constante ??

par **Mikihisa** » 15 Juin 2014, 17:30

Bonjour ! C'est tjs les problème les plus simple qui me m'embête le plus -_- !
Voici l'énoncer :
Déterminer les fonction

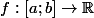
telles que

Voilà alors à première vu il s'agirait des fonction constantes positive mais comment le montrer ??? Vous pourriez me mettre sur la piste svp ?
J'ai bien conscience que

mais je sais pas ça me paraît bizarre ...
Cordialement !

par **adrien69** » 15 Juin 2014, 18:14

Yo,
Les fonctions constantes fonctionnent, pour la réciproque ça dépend de l'énoncé.

Deux possibilités, ou bien tu fais de la théorie de la mesure/intégration, et tu utilises ici des fonctions mesurables et bornées, ou bien tu ne vois pas de quoi je parle et on a encore deux choix :

Continues par morceaux bornées, ou bien continues.

Alors dans quel cadre veux-tu qu'on se place pour ta réponse ?

par **Mikihisa** » 15 Juin 2014, 19:07

Salut et merci ! Non pas de théorie de la mesure, c'est dans le cadre de l'intégration selon Riemann.
Donc dans le 2ème cadre.

par **adrien69** » 15 Juin 2014, 19:10

Mais encore, continues, ou continues par morceaux ?

par **Mikihisa** » 15 Juin 2014, 19:13

adrien69 a écrit:Mais encore, continues, ou continues par morceaux ?

Rien dans l'énoncer ne stipule sur la fonction soi continue ou même continue par morceau, mais j'ai du mal à voir comment elle ne pourrais pas être constante en fait

En fait la seule chose qu'on sait c'est qu'elle est Riemann-integrable

par **adrien69** » 15 Juin 2014, 19:20

Soit la fonction f donnée sur [0,1] par f(x)=1 pour x<1/2, 0 pour x=1/2, 1 pour x>1/2

Calcule les deux quantités.

par **Mikihisa** » 15 Juin 2014, 19:32

Sans vérifier qu'elle est bien R-intégrable on trouvera bien 1 avec la relation de châles c'est ça ? Ça serait valable pour toutes les fonctions du style avec un nombre fini de pts de discontinuité ?

par **adrien69** » 15 Juin 2014, 19:46

Exactement.

par **adrien69** » 15 Juin 2014, 19:50

Mais ne t'en fais pas, elle est bien Riemann intégrable, puisque continue par morceaux.

(C'est même une fonction en escalier, si tu autorises les singletons dans la définition)

par **adrien69** » 15 Juin 2014, 20:04

En fait la CNS que tu cherches est celle-ci :

Dans l'ensemble des fonctions continues par morceaux sur [a,b], l'égalité est vérifiée si et seulement si :

pour tout point de continuité de f, f(x)=sup|f|

THE TOOL pour faire ça consiste en le théorème de stricte positivité des intégrales : si f est supérieure ou égale à 0, et qu'il existe un point x, où f est continue, avec f(x)>0, alors l'intégrale de f est strictement positive

(théorème à compléter avec les hypothèses de régularité, l'intervalle, etc)

par **Mikihisa** » 15 Juin 2014, 20:28

Je vais chercher par la alors ! Mais si f est continue-constante par morceau et que elle est négative sur certains pts de discontinuité l'égalité reste valable non ? Du coup l'hypothèse du théorème est plus valide ? On de toute façon jvais xhecher un peu par la déjà.

Une petite question hors sujet : j'ai vu sur wiki en faisant un exo sur la non intrgabilite de la fonction indicative de Q que une fonction était Riemann intégrable si elle possédait un nombre dénombrable de pts de discontinuité (donc éventuellement infini ) est-ce que une telle fonction est considérer comme continue par morceau ??

par **adrien69** » 15 Juin 2014, 20:37

Non du tout.
Continue par morceaux induit nombre fini de discontinuités.

C'est exact, l'hypothèse du théorème ne sera plus valide, mais ce n'est pas grave. Il te suffit d'utiliser la relation de Chasles pour te ramener à un calcul sur des fonctions continues.

Enfin, tu verras, ça s'écrit bien, ce n'est pas un gros problème.

par **Ben314** » 15 Juin 2014, 20:46

adrien69 a écrit:Continue par morceaux induit nombre fini de discontinuités.

Dans le cas où le domaine de définition n'est pas un segment (par exemple R...), ce n'est pas évident du tout : je pense que dans le cas d'un intervalle quelconque I, la majorité de la littérature définit une fonction "continue par morceaux sur I" comme une fonction "continue par morceaux sur tout segment contenu dans I".
Si I n'est pas lui même un segment, il peut donc y avoir une infinité (dénombrable) de discontinuité.

Je ne évidement pas totalement certain que ce soit "la majorité" des auteurs, mais en tout cas, c'est très fréquent et donc il faut préciser la définition que l'on adopte dans le cas où I n'est pas un segment.

par **Mikihisa** » 15 Juin 2014, 20:50

Oui c'est bon je vois comment m'y prendre je pense j'avais écrire ça voire !

par **adrien69** » 15 Juin 2014, 22:02

Ben314 a écrit:Dans le cas où le domaine de définition n'est pas un segment (par exemple R...), ce n'est pas évident du tout : je pense que dans le cas d'un intervalle quelconque I, la majorité de la littérature définit une fonction "continue par morceaux sur I" comme une fonction "continue par morceaux sur tout segment contenu dans I".
Si I n'est pas lui même un segment, il peut donc y avoir une infinité (dénombrable) de discontinuité.

Je ne évidement pas totalement certain que ce soit "la majorité" des auteurs, mais en tout cas, c'est très fréquent et donc il faut préciser la définition que l'on adopte dans le cas où I n'est pas un segment.

Je suis tout à fait d'accord, mais là il travaillait sur [a,b], je ne voyais pas pourquoi compliquer les choses.

Intégration, fonction constante ??

Intégration, fonction constante ??

Qui est en ligne