Bonjour,
Je planche depuis plusieurs minutes sur le calcul du flux d'un champ vectoriel mais je suis complètement bloqué, voici l'énoncé : (Je m'excuse d'avance mais je n'ai pas réussi à utiliser l'éditeur d'équation)
Déterminer le flux doubleIntegraleFermée(F.dS) où le champ vectoriel est donné par F = x*ex + y*ey et la surface fermée satisfait la relation 3(x² + y²) + 4z² = 1
En traçant la surface sur GeoGebra j'ai constaté que la surface fermée était ellipsoïde, j'ai défini un vecteur n orthogonal à la surface défini par n = grad(F) => n = 6x*ex + 6y*ey + 8z*ez
J'ai ensuite normé ce vecteur afin qu'il soit unitaire et orthonormal à la surface, mais ensuite je suis complètement bloqué, quelqu'un aurait-t-il l'amabilité de me donner la marche à suivre ? J'imagine qu'on écrit dS comme dS = n.dS ?
Je vous remercie d'avance pour vos réponse.
Flux d’un champ de vecteurs à travers une surface fermée
8 messages
- Page 1 sur 1
Re: Flux d’un champ de vecteurs à travers une surface fermée
Bonsoir,
Pour quoi votre champs de vecteur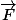 ne s'écrit pas en fonction de
ne s'écrit pas en fonction de 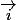 et
et 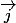
soit
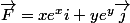
Pour quoi votre champs de vecteur
soit
Re: Flux d’un champ de vecteurs à travers une surface fermée
autre chose le Gradient est un vecteur
ex,ey et ez sont des exponentielles? ou des vecteurs?
ex,ey et ez sont des exponentielles? ou des vecteurs?
Re: Flux d’un champ de vecteurs à travers une surface fermée
Je croix comprendre ( sans Latex c'est pas toujours facile, sorry),ex, ey et ez sont des vecteurs
vous pouvez calculer la divergence de F et si votre courbe S est une surface orientée fermée
et appliquer Théorème de Gauss-Ostrogradski
vous pouvez calculer la divergence de F et si votre courbe S est une surface orientée fermée
et appliquer Théorème de Gauss-Ostrogradski
Re: Flux d’un champ de vecteurs à travers une surface fermée
autre chose, le gradient se calcule sur des champs scalaire donc par sur F ( si c'est un vecteur), vous vouliez dire S ?, par contre la divergence se calcule sur des vecteurs.?
Re: Flux d’un champ de vecteurs à travers une surface fermée
ex,et et ez sont les vecteurs unitaires
Re: Flux d’un champ de vecteurs à travers une surface fermée
Bonjour,
la surface fermée 3(x² + y²) + 4z² = 1 est une ellipsoïde de e révolution de révolution d’axe 0z
: , de la forme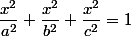
paramétrez cette ellipsoïde en coordonnées sphériques.
la surface fermée 3(x² + y²) + 4z² = 1 est une ellipsoïde de e révolution de révolution d’axe 0z
: , de la forme
paramétrez cette ellipsoïde en coordonnées sphériques.
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 21 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
