Famille de polynômes de degré différent libre

[Deura]

Bonjour,
Je dois résoudre cet exercice :

Montrer que toute famille finie (Pi)1≤i≤m de polynômes non nuls, de degrés deux à deux distincts, est libre.

Je sais personnellement que cela est vrai si la famille est échelonnée en degré. Mais là ce n'est pas le cas.
L'affirmation semble logique, mais comment la démontrer ?

Merci pour votre aide et bonne rentrée

[capitaine nuggets]

Salut !

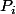
Quitte à ré-indexer les pour que les degré soient rangés par ordre croissant ou décroissant, tu peux supposer sans perte de généralité que la famille est échelonnée en degré.

Bonne rentrée !