Famille libre de polynômes
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
magnum
- Membre Relatif
- Messages: 149
- Enregistré le: 22 Avr 2007, 09:12
-
 par magnum » 03 Sep 2008, 18:17
par magnum » 03 Sep 2008, 18:17
bonjour,
Je cherche à montrer que la famille suivant est libre mais je n'y arrive pas
( (1+X)^n, X(1+X)^(n-1), X²(1+X)^(n-2) ...., X^n))
j'essaie de dériver , évaluer en des pts mais ça ne marche pas .
Merci d'avance !
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 03 Sep 2008, 18:30
par Doraki » 03 Sep 2008, 18:30
Une récurrence ça marche bien.

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 03 Sep 2008, 18:36
par leon1789 » 03 Sep 2008, 18:36
...ou directement (si on connait le déterminant de van der monde) en divisant tous les polynômes par X^n (et travailler dans le corps Q(X) ).
-
magnum
- Membre Relatif
- Messages: 149
- Enregistré le: 22 Avr 2007, 09:12
-
 par magnum » 03 Sep 2008, 19:51
par magnum » 03 Sep 2008, 19:51
tu pourrais détailler la récurrence STp en le faisant je vois que ça ne marche pas très bien.
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 03 Sep 2008, 19:58
par Doraki » 03 Sep 2008, 19:58
Suppose que tu aies a0.X^n + a1.(1+X).X^(n-1) + ... + an.(1+X)^n = 0.
Ca veut dire X[ a0.X^(n-1) + ... + a(n-1).(1+X)^(n-1)] + an.(1+X)^n = 0
Montre d'abord que an est nul, ensuite tu pourras te ramener à l'intérieur du crochet, c'est-à-dire, le cas (n-1).
-
magnum
- Membre Relatif
- Messages: 149
- Enregistré le: 22 Avr 2007, 09:12
-
 par magnum » 03 Sep 2008, 20:39
par magnum » 03 Sep 2008, 20:39
merci j'ai réussi à prouver qu'elle était libre et donc une base de Rn[X]. J'ai réussi à trouver les coordonnées de 1 dans cette base.
On me demande d'en déduire les coordonnées de X^(n-k) et de X^p pour p entre 1et n et là je bloque. Merci de ton aide.
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 03 Sep 2008, 20:43
par Doraki » 03 Sep 2008, 20:43
euh.. X^p = X^p * 1 ?
Suffit alors de remplacer 1 par un truc bien.
-
magnum
- Membre Relatif
- Messages: 149
- Enregistré le: 22 Avr 2007, 09:12
-
 par magnum » 03 Sep 2008, 20:49
par magnum » 03 Sep 2008, 20:49
lol désolé mais je ne comprend pas .
pour déterminer les coordonnées de 1 j'ai écrit
(1+X-X)^n et j'ai développé mais après ?

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 03 Sep 2008, 21:41
par leon1789 » 03 Sep 2008, 21:41
magnum a écrit:lol désolé mais je ne comprend pas .
pour déterminer les coordonnées de 1 j'ai écrit
(1+X-X)^n et j'ai développé mais après ?
Même ruse, mais un cran en dessous
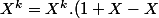^{n-k})
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 69 invités
