Factorisation d'un polynômes de degré 4..
18 messages
- Page 1 sur 1
factorisation d'un polynômes de degré 4..
Bonsoir,
on me demande de factoriser au maximum le polynôme de degé 4 suivant:
P(X)= X^4+9X²+15X+7
en notant les racines:a,b,c,d
j'ai les relations suivantes:
a+b+c+d=0
abcd=7
ab+cd+(a+b)(c+d)=9
ab(c+d)+cd(a+b)=-15
on constate alors que
P(X)=(X²-(a+b)X+ab)(X²+(a+b)X+cd)
mais après je ne vois plus trop comment faire... :hein:
est-ce que quelqu'un pourrait m'aider s'il vous plaît?
merci d'avance :++:
on me demande de factoriser au maximum le polynôme de degé 4 suivant:
P(X)= X^4+9X²+15X+7
en notant les racines:a,b,c,d
j'ai les relations suivantes:
a+b+c+d=0
abcd=7
ab+cd+(a+b)(c+d)=9
ab(c+d)+cd(a+b)=-15
on constate alors que
P(X)=(X²-(a+b)X+ab)(X²+(a+b)X+cd)
mais après je ne vois plus trop comment faire... :hein:
est-ce que quelqu'un pourrait m'aider s'il vous plaît?
merci d'avance :++:
les formules exactes donnant les racines sont assez compliquées. Peut être peux tu séparer les racines réelles par une méthode d'analyse de Terminale (étude de P' et P") puis en calculer des valeurs approchées par la méthode itérative de Newton.
Parce que les formules exactes des racines semblent très compliquées !!! Que veux tu faire au juste avec cette factorisation ?
Ps: séparer les racines veut dire . trouver des intervalles comprenant chacun une racine isolée.
Parce que les formules exactes des racines semblent très compliquées !!! Que veux tu faire au juste avec cette factorisation ?
Ps: séparer les racines veut dire . trouver des intervalles comprenant chacun une racine isolée.
en fait,je suis à l'iufm en préparation capes.
et pendant l'exposé sur les polynômes,notre formatrice nous a demandé de déterminer les racines de ce polynôme...
et comme c'est assez long,elle nous demande de le terminer chez nous.
mais je crois que je vais laisser tomber et travailler autre chose parce que j'ai l'impression de perdre mon temps là...
merci beaucoup! je note tout ce que tu m'as dit Mathelot!:++:
et pendant l'exposé sur les polynômes,notre formatrice nous a demandé de déterminer les racines de ce polynôme...
et comme c'est assez long,elle nous demande de le terminer chez nous.
mais je crois que je vais laisser tomber et travailler autre chose parce que j'ai l'impression de perdre mon temps là...
merci beaucoup! je note tout ce que tu m'as dit Mathelot!:++:
on veut résoudre l'équation 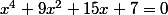
pour résoudre cette équation du 4ème degré, on considère l'inconnue x
et on cherche une quantité y telle que:
^2) soit égale à un trinome de discriminant nul. En effet, un trinome de discriminant nul est un carré de la forme
soit égale à un trinome de discriminant nul. En effet, un trinome de discriminant nul est un carré de la forme ^2) et l'on aura donc ensuite à résoudre l'équation:
et l'on aura donc ensuite à résoudre l'équation: ^2= (ax+b)^2) , c'est à dire deux équations du second degré.
, c'est à dire deux équations du second degré.
^2=x^4+2yx^2+y^2=(-9x^2-15x-7)+2yx^2+y^2)
^2=x^2(-9+2y)-15x-7+y^2)
écrivons que le second membre a son discriminant nul:
(-7+y^2)=0)
cette équation équivaut à l'équation:
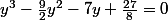
on trouvera demain une racine réelle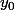 par la méthode de Cardan. :dodo:
par la méthode de Cardan. :dodo:
pour résoudre cette équation du 4ème degré, on considère l'inconnue x
et on cherche une quantité y telle que:
écrivons que le second membre a son discriminant nul:
cette équation équivaut à l'équation:
on trouvera demain une racine réelle
Bon, on voit voir que ça sent le roussi...
je fais un changement de variable:
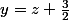
pour aboutir à une équation du 3ème degré sans terme en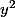
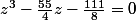
on pose:
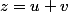 selon la méthode de Cardan pour résoudre les équation de degré 3:
selon la méthode de Cardan pour résoudre les équation de degré 3:
on obtient:
(3uv-\frac{55}{4})=0)
pour trouver une racine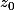 , il SUFFIT que:
, il SUFFIT que:
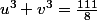
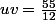
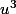 et
et 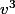 sont les solutions de l'équation:
sont les solutions de l'équation:
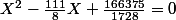
d'ou, les deux racines complexes conjuguées:
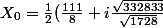=u^3)
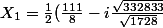=v^3)
On calcule le module du nombre complexe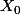
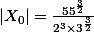
d'où:
On peut prendre pour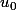 et
et 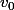 :
:
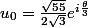
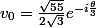
où:
=\frac{333 \sqrt{3}}{110 \sqrt{55}})
=\frac{\sqrt{998499}}{110 \sqrt{165}})
d'où:
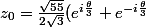)
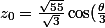)
soit encore:
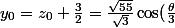+\frac{3}{2})
Les quatre racines du polynome P initial sont les racines des deux équations
du second degré d'inconnue x:
=0)
=0)
où:
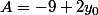
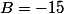
l'ennui, c'est que la quantité est proche de zéro.
est proche de zéro.
je vais regarder s'il n'y a pas une ruse...
je fais un changement de variable:
pour aboutir à une équation du 3ème degré sans terme en
on pose:
on obtient:
pour trouver une racine
d'ou, les deux racines complexes conjuguées:
On calcule le module du nombre complexe
d'où:
On peut prendre pour
où:
d'où:
soit encore:
Les quatre racines du polynome P initial sont les racines des deux équations
du second degré d'inconnue x:
où:
l'ennui, c'est que la quantité
je vais regarder s'il n'y a pas une ruse...
Regardons une seconde méthode, dite "de Descartes".
Nous cherchons à factoriser
=x^4+9x^2+15x+7) sous la forme:
sous la forme:
(x^2-ax+c))
L'identification des coefficients donne les relations:
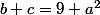
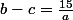
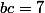
l'identité triviale supplémentaire:
^2=(b-c)^2+4bc)
donne en remplaçant une équation bicarrée de degré 6:
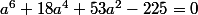
en posant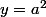
on obtient une équation du troisième degré:
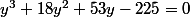
En résolvant cette dernière équation par la méthode de Cardan, celle çi n'a qu'une solution réelle positive et on retrouve les solutions trouvées.
Nous cherchons à factoriser
L'identification des coefficients donne les relations:
l'identité triviale supplémentaire:
donne en remplaçant une équation bicarrée de degré 6:
en posant
on obtient une équation du troisième degré:
En résolvant cette dernière équation par la méthode de Cardan, celle çi n'a qu'une solution réelle positive et on retrouve les solutions trouvées.
18 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 52 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
