Factorisation de polynômes
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
kkk
- Membre Relatif
- Messages: 242
- Enregistré le: 23 Sep 2006, 18:05
-
 par kkk » 13 Jan 2007, 13:48
par kkk » 13 Jan 2007, 13:48
Bonjour,
J'ai du mal à mettre :
a=X
b=X^2-1
c=X^3-2X
d=X^4 - 2X -X^2 -1
en produit de facteurs irréductibles dans R[X]
Pourriez-vous maider ?
merci
kkk
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 13 Jan 2007, 13:54
par Flodelarab » 13 Jan 2007, 13:54
a) sans commentaires.
b) Rappel toi la classe de 3eme (pour qqun qui poste dans le supérieur ...)
c) racine évidente et rebelote (comme le b)
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 13 Jan 2007, 13:55
par Joker62 » 13 Jan 2007, 13:55
Les facteurs irréductibles dans |R sont de la forme :
P(x) = x - a
P(x) = x² + ax + b sans racine réelle
J'vois pas de difficulté à proprement parler
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 13 Jan 2007, 13:57
par Zebulon » 13 Jan 2007, 13:57
Bonjour,
kkk a écrit:a=X
est irréductible
b=X^2-1
a²-b²...
c=X^3-2X
c=X(X²-2) et a²-b².
d=X^4 - 2X -X^2 -1
Je ne sais pas...
-
bitonio
- Membre Rationnel
- Messages: 764
- Enregistré le: 28 Mai 2006, 15:29
-
 par bitonio » 13 Jan 2007, 13:59
par bitonio » 13 Jan 2007, 13:59
le d) c'est (x^2+x+1)(x^2-x-1)
-
Epsilon
- Membre Relatif
- Messages: 175
- Enregistré le: 08 Nov 2006, 14:23
-
 par Epsilon » 13 Jan 2007, 13:59
par Epsilon » 13 Jan 2007, 13:59
pour la 4éme
x^4-2x-x^2-1 = x^4-(x^2+2x+1)=x^4-(x+1)^2=(x^2-(x+1))(x^2+x+1)
donc
x^4-2x-x^2-1=(x^2-x-1)(x^2+x+1)
-
kkk
- Membre Relatif
- Messages: 242
- Enregistré le: 23 Sep 2006, 18:05
-
 par kkk » 13 Jan 2007, 19:09
par kkk » 13 Jan 2007, 19:09
merci !
kkk
-
praud
- Membre Relatif
- Messages: 175
- Enregistré le: 28 Mai 2006, 20:33
-
 par praud » 13 Jan 2007, 19:44
par praud » 13 Jan 2007, 19:44
^2 - \frac{1}<br />{4} - 1 \cr <br /> = (x - \frac{1}<br />{2})^2 - \frac{5}<br />{4} \cr <br /> = (x - \frac{1}<br />{2} + \frac{{\sqrt 5 }}<br />{2})(x - \frac{1}<br />{2} - \frac{{\sqrt 5 }}<br />{2}) \cr)
donc on peut dire que
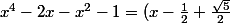(x - \frac{1}<br />{2} - \frac{{\sqrt 5 }}<br />{2})(x^2 + x + 1) \cr)
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 13 Jan 2007, 19:57
par Flodelarab » 13 Jan 2007, 19:57
praud a écrit:^2 - \frac{1}<br />{4} - 1 \cr <br /> = (x - \frac{1}<br />{2})^2 - \frac{5}<br />{4} \cr <br /> = (x - \frac{1}<br />{2} + \frac{{\sqrt 5 }}<br />{2})(x - \frac{1}<br />{2} - \frac{{\sqrt 5 }}<br />{2}) \cr)
donc on peut dire que
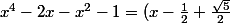(x - \frac{1}<br />{2} - \frac{{\sqrt 5 }}<br />{2})(x^2 + x + 1) \cr)
:++: Bien vu !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 28 invités
