Racines et factorisation de polynômes.
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Serena2095
- Membre Naturel
- Messages: 34
- Enregistré le: 06 Oct 2012, 19:00
-
 par Serena2095 » 12 Oct 2012, 11:48
par Serena2095 » 12 Oct 2012, 11:48
Bonjour, pouvez vous m'aider à résoudre cet exercice de factorisation s'il vous plaît?
Je dois factoriser et trouver les racines des polynômes suivants:
P(x)=x^4+2X^3+2x^2+2x+1
Q(x)=x^4-6x^2+8x-3
Merci d'avance pour votre aide.
-
ThekamikazeFou
- Membre Relatif
- Messages: 403
- Enregistré le: 12 Juin 2012, 15:26
-
 par ThekamikazeFou » 12 Oct 2012, 11:56
par ThekamikazeFou » 12 Oct 2012, 11:56
Serena2095 a écrit:Bonjour, pouvez vous m'aider à résoudre cet exercice de factorisation s'il vous plaît?
Je dois factoriser et trouver les racines des polynômes suivants:
P(x)=x^4+2X^3+2x^2+2x+1
Q(x)=x^4-6x^2+8x-3
Merci d'avance pour votre aide.
Pour p(x) il y a -1 comme racine evidente. Apres utilise la methode de horner et tu trouve un polynome du second degres que tu resouds.
Pour la second tu fais pareil avec 1 comme racine evidente..

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 12 Oct 2012, 13:06
par chan79 » 12 Oct 2012, 13:06
ThekamikazeFou a écrit:Pour p(x) il y a -1 comme racine evidente. Apres utilise la methode de horner et tu trouve un polynome du second degres que tu resouds.
Pour la second tu fais pareil avec 1 comme racine evidente..
Pour P, on peut voir que i et -i sont solutions; on a donc comme facteur (x²+1)
-
fibonacci
- Membre Relatif
- Messages: 492
- Enregistré le: 21 Mai 2006, 08:50
-
 par fibonacci » 12 Oct 2012, 15:37
par fibonacci » 12 Oct 2012, 15:37
bonjour;
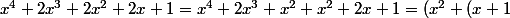)^2)

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 12 Oct 2012, 15:56
par chan79 » 12 Oct 2012, 15:56
fibonacci a écrit:bonjour;
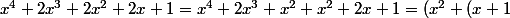)^2)
Bonne idée de remplacer 2x² par x²+x²
Pour le résultat, je dirais plutôt
x;)+2x³+2x²+2x+1=(x+1)²(x²+1)
-
fibonacci
- Membre Relatif
- Messages: 492
- Enregistré le: 21 Mai 2006, 08:50
-
 par fibonacci » 12 Oct 2012, 16:18
par fibonacci » 12 Oct 2012, 16:18
chan79 a écrit:Bonne idée de remplacer 2x² par x²+x²
Pour le résultat, je dirais plutôt
x;)+2x³+2x²+2x+1=(x+1)²(x²+1)
ma mise en facteur est incorrecte mais son développement est à rapprocher à
^2)
avec
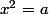
et
=b)
^2+2(x^2(x+1))+(x+1)^2=x^4+2x^3+2x^2+x^2+2x+1=x^4+2x^3+3x^2+2x+1)
et comme il y a un

en trop
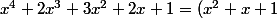^2)

^2-x^2=(x^2+x+1-(x))(x^2+x+1+(x)))
-
ThekamikazeFou
- Membre Relatif
- Messages: 403
- Enregistré le: 12 Juin 2012, 15:26
-
 par ThekamikazeFou » 12 Oct 2012, 19:49
par ThekamikazeFou » 12 Oct 2012, 19:49
Vous vous compliquez la vie, m'enfin bon... Si ça fonctionne :)
-
fibonacci
- Membre Relatif
- Messages: 492
- Enregistré le: 21 Mai 2006, 08:50
-
 par fibonacci » 13 Oct 2012, 03:46
par fibonacci » 13 Oct 2012, 03:46
Bonjour;
ThekamikazeFou a écrit:Vous vous compliquez la vie, m'enfin bon... Si ça fonctionne

pas plus compliqué que Horner
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 25 invités
