Factorielle
19 messages
- Page 1 sur 1
Factorielle
Bonjour,
Je me heurte a une difficulte. J`essaie d`ecrire les factorielles sous forme de somme.
Exemple :
5!= 1^x+2^x+3^x+4^x+5^x (ou est x est une variable reelle dependant de n)
je trouve les valeurs approchees suivantes :
la premiere colonne represente le "n" de la factorielle
la seconde la valeur
2 0
3 1
4 1.808
5 2.57
6 3.302
7 4.04
8 4.7828
pour n=2 x=0
2!=1^0+2^0=2
2!=2
pour n=3
x=1
3!=1^1+2^1+3^1=6
3!=6
pour n=4
x a peu pres egal a 1.808
4!=1^1.808+2^1.808+3^1.808+4^1.808
4!=24.05 approchant 24
bref, j`ai fait le calcul jusqu`a 8!
avec les valeurs approchees suivantes de x
5! x=2.5700
6! x=3.3020
7! x=4.0400
8! x=4.7280
J`ai vu que x evoluait en fonction de n
Je suppose donc qu`il devrait y avoir une fonction plus precise de x fonction de n
Comme je travaille sur excel je n`ai pas pu aller au dela de factorielle 8!
Je demande de l`aide pour pouvoir aller au moins jusqu`a n=100 pour avoir une idee de la courbe x.
Merci pour toute aide.
Desole, je ne maitrise pas le latex.
Si vous avez compris le principe je peux en revanche lire le latex et je vous dirai que cela correspond a mon idee.
Merci.
Je me heurte a une difficulte. J`essaie d`ecrire les factorielles sous forme de somme.
Exemple :
5!= 1^x+2^x+3^x+4^x+5^x (ou est x est une variable reelle dependant de n)
je trouve les valeurs approchees suivantes :
la premiere colonne represente le "n" de la factorielle
la seconde la valeur
2 0
3 1
4 1.808
5 2.57
6 3.302
7 4.04
8 4.7828
pour n=2 x=0
2!=1^0+2^0=2
2!=2
pour n=3
x=1
3!=1^1+2^1+3^1=6
3!=6
pour n=4
x a peu pres egal a 1.808
4!=1^1.808+2^1.808+3^1.808+4^1.808
4!=24.05 approchant 24
bref, j`ai fait le calcul jusqu`a 8!
avec les valeurs approchees suivantes de x
5! x=2.5700
6! x=3.3020
7! x=4.0400
8! x=4.7280
J`ai vu que x evoluait en fonction de n
Je suppose donc qu`il devrait y avoir une fonction plus precise de x fonction de n
Comme je travaille sur excel je n`ai pas pu aller au dela de factorielle 8!
Je demande de l`aide pour pouvoir aller au moins jusqu`a n=100 pour avoir une idee de la courbe x.
Merci pour toute aide.
Desole, je ne maitrise pas le latex.
Si vous avez compris le principe je peux en revanche lire le latex et je vous dirai que cela correspond a mon idee.
Merci.
Re: Factorielle
Desole de l`oubli. Juste une question : quelqu`un a-t-il aborde la question de cette maniere? cela economiserait les echanges en cas d`existence d`une documentation relative a la question. Le but est d`aboutir a une formulation plus precise, je presume que x est en relation tres etroite avec n. Une centaine de valeurs de n egal a 1 jusqu`a 100 me permettrait d`orienter mes recherches.
Merci pour votre aide.
Merci pour votre aide.
Re: Factorielle
Excel te permet de calculer n! jusqu'à n=170.
Certes il y a des micro-erreurs, mais pour ton usage, ça me paraît largement suffisant.
Comme tu écris x avec 5 ou 6 décimales seulement, l'approximation sur x est largement plus grave que l'approximation faite par Excel dans le calcul de la factorielle.
Et si tu veux aller au delà, très au-delà, tu peux très facilement calculer log(n!) ... et tu peux aussi calculer le logarithme de ton 2ème membre. Encore que, pas sûr finalement que ce soit si simple que ça pour le 2ème membre.
Certes il y a des micro-erreurs, mais pour ton usage, ça me paraît largement suffisant.
Comme tu écris x avec 5 ou 6 décimales seulement, l'approximation sur x est largement plus grave que l'approximation faite par Excel dans le calcul de la factorielle.
Et si tu veux aller au delà, très au-delà, tu peux très facilement calculer log(n!) ... et tu peux aussi calculer le logarithme de ton 2ème membre. Encore que, pas sûr finalement que ce soit si simple que ça pour le 2ème membre.
Re: Factorielle
Merci.
Ce que je cherche ce n`est pas la valeur approchee ou exacte de n!
Il y a le calcul direct et les approximations (Stirling, Ramanujan etc.._)
Ce que je cherche ce sont les valeurs successives de x variable reelle laquelle est fonction de n.
Pour chaque factorielle n! je dois calculer une valeur approche de x. Aussi precise que possible.
En consequence, je pourrais expliciter toute factorielle avec ce "x".
Une somme similaire a la fonction zeta de Riemann avec zeta de s variant pour chaque n. On ne fait pas varier a l`infini mais jusqu`a atteindre la valeur de n.
On devrait resoudre par exemple :
pour 20!=1^x+2^x+3^x+........+19^x+20^x
et a chaque fois pour chaue factorielle calculer la valeur de x.
On peut obtenir une valeur exacte a n! en prenant la valeur entiere de cette sommation.
Cela demande un programme informatique (je suis nul en informatique et trop vieux pour cela).
Merci pour toute aide.
Ce que je cherche ce n`est pas la valeur approchee ou exacte de n!
Il y a le calcul direct et les approximations (Stirling, Ramanujan etc.._)
Ce que je cherche ce sont les valeurs successives de x variable reelle laquelle est fonction de n.
Pour chaque factorielle n! je dois calculer une valeur approche de x. Aussi precise que possible.
En consequence, je pourrais expliciter toute factorielle avec ce "x".
Une somme similaire a la fonction zeta de Riemann avec zeta de s variant pour chaque n. On ne fait pas varier a l`infini mais jusqu`a atteindre la valeur de n.
On devrait resoudre par exemple :
pour 20!=1^x+2^x+3^x+........+19^x+20^x
et a chaque fois pour chaue factorielle calculer la valeur de x.
On peut obtenir une valeur exacte a n! en prenant la valeur entiere de cette sommation.
Cela demande un programme informatique (je suis nul en informatique et trop vieux pour cela).
Merci pour toute aide.
Re: Factorielle
c'est marrant on dirait pile poil une droite
pour 9! j'ai trouvé environ x = 5,5271
pour 10! x= 6,27491
pour 11! x=7,02622
mais c'est long à calculer
tu fais comment pour trouver x, en tatonnant ou tu as une méthode plus rapide ?

EDIT
jusqu'à 25! mais valeurs à vérifier
pour 9! j'ai trouvé environ x = 5,5271
pour 10! x= 6,27491
pour 11! x=7,02622
mais c'est long à calculer
tu fais comment pour trouver x, en tatonnant ou tu as une méthode plus rapide ?

EDIT
jusqu'à 25! mais valeurs à vérifier
- Code: Tout sélectionner
N=4 x=1,806 somme=24,0235612680506 factorielle=24
N=5 x=2,56 somme=120,062175747768 factorielle=120
N=6 x=3,301 somme=720,065949382907 factorielle=720
N=7 x=4,041 somme=5045,11775730639 factorielle=5040
N=8 x=4,782 somme=40338,7813212003 factorielle=40320
N=9 x=5,527 somme=363530,577147806 factorielle=362880
N=10 x=6,274 somme=3629162,52084329 factorielle=3628800
N=11 x=7,026 somme=39988337,309366 factorielle=39916800
N=12 x=7,78 somme=479176847,101031 factorielle=479001600
N=13 x=8,538 somme=6232351970,66812 factorielle=6227020800
N=14 x=9,299 somme=87297119040,1326 factorielle=87178291200
N=15 x=10,063 somme=1310763988024,81 factorielle=1307674368000
N=16 x=10,829 somme=20957062301294 factorielle=20922789888000
N=17 x=11,598 somme=356503136540839 factorielle=355687428096000
N=18 x=12,369 somme=6,41519814966807E+15 factorielle=6,402373705728E+15
N=19 x=13,142 somme=1,21779416361295E+17 factorielle=1,21645100408832E+17
N=20 x=13,918 somme=2,43993438334355E+18 factorielle=2,43290200817664E+18
N=21 x=14,695 somme=5,11847277443884E+19 factorielle=5,10909421717094E+19
N=22 x=15,474 somme=1,125318214225E+21 factorielle=1,12400072777761E+21
N=23 x=16,255 somme=2,5883538836381E+22 factorielle=2,5852016738885E+22
N=24 x=17,038 somme=6,2186801289608E+23 factorielle=6,20448401733239E+23
N=25 x=17,822 somme=1,55343145846657E+25 factorielle=1,5511210043331E+25
Modifié en dernier par danyL le 09 Juin 2020, 22:07, modifié 4 fois.
Re: Factorielle
Merci.
Pour le moment je tatonne tout en sachant qu`il existe des algorithmes (derives de Newton) qui permettent une solution approchee rapide. Comme je suis nul en informatique (pas vraiment nul en fait), je me contente d`exposer mon idee. Une telle approche a-t-elle deja ete faite? Je n`en sais rien. Je supoose qu`il existe des outils permettant d`avoir x fonction de n sous une forme explicite.
Peut-etre que des internautes mieux outilles se manifesteront. Je les en remercie d`avance.
Pour le moment je tatonne tout en sachant qu`il existe des algorithmes (derives de Newton) qui permettent une solution approchee rapide. Comme je suis nul en informatique (pas vraiment nul en fait), je me contente d`exposer mon idee. Une telle approche a-t-elle deja ete faite? Je n`en sais rien. Je supoose qu`il existe des outils permettant d`avoir x fonction de n sous une forme explicite.
Peut-etre que des internautes mieux outilles se manifesteront. Je les en remercie d`avance.
Re: Factorielle
Merci beaucoup DanyL pour les calculs jusqu`a 25.
En reflechissant un peu plus apres un sommeil agite, je change de fusil d`epaule et je m`oriente desormais vers une autre piste.
A supposer que je debouche sur une formulation explicite de x en fonction de n, je ne pourrais pas en faire un usage pratique. Meme en reformulant mon equation de maniere a avoir un resultat exact en prenant la valeur entiere de la somme mon but ne serait pas atteint.
Je devrai passer par un autre chemin.
On a invente le logarithme et il est temps de creer une nouvelle appellation ou fonction pour travailler sur des nombres gigantesques et precis (nombres de plusieurs milliards de chiffres). J`y reflechis avec mes modestes moyens (papier,crayon).
Merci mille fois.
En reflechissant un peu plus apres un sommeil agite, je change de fusil d`epaule et je m`oriente desormais vers une autre piste.
A supposer que je debouche sur une formulation explicite de x en fonction de n, je ne pourrais pas en faire un usage pratique. Meme en reformulant mon equation de maniere a avoir un resultat exact en prenant la valeur entiere de la somme mon but ne serait pas atteint.
Je devrai passer par un autre chemin.
On a invente le logarithme et il est temps de creer une nouvelle appellation ou fonction pour travailler sur des nombres gigantesques et precis (nombres de plusieurs milliards de chiffres). J`y reflechis avec mes modestes moyens (papier,crayon).
Merci mille fois.
Re: Factorielle
tournesol a écrit:Question : connais tu la formule de Stirling ?
Oui et celle de Ramanujan et d`autres, mais ce n`est pas cela que je cherche. Merci.
Re: Factorielle
tournesol a écrit:Avec une CASIO graph 35+
x(1000!)=855,78823...
Probablement vrai puisque quand devient tres grand x tend n (x/n tend lentement vers un nombre de proche de 1).
Quand n est egal a une certaine fonction de k, je peux exprimer factorielle n avec des puissances et des factorielles tres inferieurs a n. Je vais retrouver mes formules et je les posterai. Je dois fouiller dans mes posts d`il y a plus de 10 ans sur un forum americain.
Merci et a bientot.
Re: Factorielle
toujours avec casio : x(10000!)=8914,8062...
Il semblerait (heuristique avec une intégrale et Stirling mais pas démo) que x(n!) soit equivalent à n .
Il semblerait (heuristique avec une intégrale et Stirling mais pas démo) que x(n!) soit equivalent à n .
Re: Factorielle
A l'aide d'encadrement par des intégrales on obtient facilement
=n-\frac{n}{lnn}+O(1))
Appliquée à n=10000 , on obtient une erreur relative inférieure à 0,01% .
Appliquée à n=10000 , on obtient une erreur relative inférieure à 0,01% .
Re: Factorielle
Une idee m`est venue a l`esprit.
Comme x tend vers n tres lentement il est fort possible que x soit une valeur entiere.
On aurait de ce fait pour une factorielle n! a trouver telle que x soit exactement egal a une valeur entiere. Les deuz membres doivent etre identiques, ce qui presuppose que l`on calcule la factorielle de maniere exacte et non approximative. Je crois que c`est possible et ce serait merveilleux d`avoir cette valeur entiere de x. Ce serait un bon point de depart. J`essaie d`imaginer la taille de ce chiffre.
Comme x tend vers n tres lentement il est fort possible que x soit une valeur entiere.
On aurait de ce fait pour une factorielle n! a trouver telle que x soit exactement egal a une valeur entiere. Les deuz membres doivent etre identiques, ce qui presuppose que l`on calcule la factorielle de maniere exacte et non approximative. Je crois que c`est possible et ce serait merveilleux d`avoir cette valeur entiere de x. Ce serait un bon point de depart. J`essaie d`imaginer la taille de ce chiffre.
Re: Factorielle
tous les calculs numériques effectués sur ce fil ont montré que x(n!) n'est pas entier .
Re: Factorielle
J`avais parle d`une autre identite que j`avais creee il y a quelques annees.
Si on peut ecrire n=(3*k)+1 on peut ecrire :
n!=(3^k)*k!*Produit ((3i)^2-1) avec i variant de i=1 a i=k
et on peut par recursion avoir une formule compliquee en remplacant k par (3*k`+1) et ainsi de suite jusqu`a obtenir ce que l`on veut. C`est facile a faire une fois que l`on a la formule de base citee precedemment.
J`ai d`autres formules basees sur le meme principe avec n=a*k+b.
Comme j`ai des difficultes avec l`ecriture en latex, je ne pourrai malheureusement pas ecrire la formule de maniere plus lisible. Desole.
Si on peut ecrire n=(3*k)+1 on peut ecrire :
n!=(3^k)*k!*Produit ((3i)^2-1) avec i variant de i=1 a i=k
et on peut par recursion avoir une formule compliquee en remplacant k par (3*k`+1) et ainsi de suite jusqu`a obtenir ce que l`on veut. C`est facile a faire une fois que l`on a la formule de base citee precedemment.
J`ai d`autres formules basees sur le meme principe avec n=a*k+b.
Comme j`ai des difficultes avec l`ecriture en latex, je ne pourrai malheureusement pas ecrire la formule de maniere plus lisible. Desole.
Re: Factorielle
Salut,
Je poste une image dans laquelle il y a une formule mathematique :
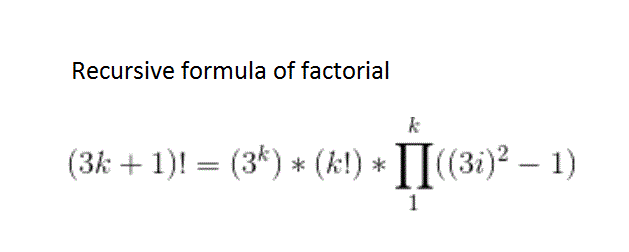
Je voudrai savoir si la formule est exacte et si on peut par recursion la developper en remplacer k par (3*k`)+1 recursivement (en bref la developper).
Merci
Je poste une image dans laquelle il y a une formule mathematique :
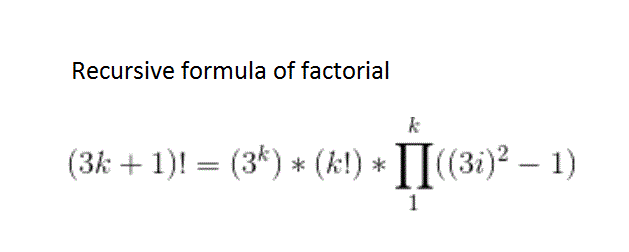
Je voudrai savoir si la formule est exacte et si on peut par recursion la developper en remplacer k par (3*k`)+1 recursivement (en bref la developper).
Merci
Re: Factorielle
Dans cette formule, on voit une différence de 2 carrés, ça se factorise facilement. Et visiblement, avec 2 ou 3 manipulations assez simples, on conclue que cette égalité est exacte, ce n'est pas approximation.
19 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 52 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
