Bonjour, j'ai un doute quant à la résolution de l'exercice (et la rigeur de la justification que j'y apporte si j'ai raison)
Je dirais
A=([0,2]\Q) inter [2;3[
donc A = {2\Q}
or 2 appartient à Q, donc A = le vide
Alors
sup A = inf A = max A = min A = le vide
Merci d'avance
(L2) exo d'ensembles (bornes sup,inf,minimum,maximum)
6 messages
- Page 1 sur 1
Re: (L2) exo d'ensembles (bornes sup,inf,minimum,maximum)
Salut !
Attention !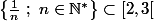 mais on n'a pas égalité. Montre alors que
mais on n'a pas égalité. Montre alors que }) . Je te laisse conclure.
. Je te laisse conclure.
Je rappelle que dans , la borne supérieure (resp. inférieure) est à valeur dans
, la borne supérieure (resp. inférieure) est à valeur dans 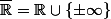 .
.
Attention !
Je rappelle que dans
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Re: (L2) exo d'ensembles (bornes sup,inf,minimum,maximum)
Salut,
Ca sent la "coquille" dans l'énoncé à plein nez (ou alors le type qui a fait l'exo. est réellement vicieux....)
Sinon, effectivement l'ensemble A est vide et je ne pense pas qu'il y ait vraiment besoin de calculs pour le voir : A est défini comme l'intersection de deux ensembles, le premier ne contenant aucun rationnels et le second ne contenant que des rationnels donc A est vide.
Par contre ta rédaction n'est pas terrible du tout :
- Ton premier = n'est, à priori, pas une égalité mais une inclusion vu que l'ensemble des 3-1/n avec n entier n'est évidement pas égal à [2,3[. La démarche fonctionne tout de même vu qu'au lieu d'obtenir que A est égal à l'ensemble vide, tu devrait obtenir que A est inclu dans l'ensemble vide, mais au final, ça revient au même.
- Ensuite, plus grave, si A est vide, alors "sup(A), max(A),..." ne sont surement pas égaux à "le vide" pour la bonne et simple raison que ces trucs (Sup, Max, ...), lorsqu'ils existent, ce sont des réels et que "le vide", c'est pas du tout un réel. Donc la conclusion finale, c'est qu'aucun d'entre eux n'existe.
Il faut évidement faire la différence entre le fait qu'un "truc" n'existe pas et le fait que le truc en question est vide : il n'y a aucun doute concernant le fait que "le vide", ça existe (en tout cas en math).
A mon avis, c'est une erreur lié au fait qu'au Lycée, de façon mécanique et sans réfléchir, lorsque l'on demande à des élèves de résoudre une équation, ils terminent leur prose par S=... avec, comme toujours, aucune phrase d'explication sur ce que désigne S.
Si une équation, par exemple f(x)=0 n'a pas de solutions, ça signifie qu'il n'existe pas de x tel que f(x)=0, mais par contre, l'ensemble des solutions, c'est à dire l'ensemble des x vérifiant f(x)=0, lui il existe (et il est vide).
Pour prendre une analogie dans la vie courante, si un panier est vide, alors ce qui n'existe pas, c'est un objet qui soit à l'intérieur du panier. Par contre, le panier, bien que vide, lui il existe...
Ca sent la "coquille" dans l'énoncé à plein nez (ou alors le type qui a fait l'exo. est réellement vicieux....)
Sinon, effectivement l'ensemble A est vide et je ne pense pas qu'il y ait vraiment besoin de calculs pour le voir : A est défini comme l'intersection de deux ensembles, le premier ne contenant aucun rationnels et le second ne contenant que des rationnels donc A est vide.
Par contre ta rédaction n'est pas terrible du tout :
- Ton premier = n'est, à priori, pas une égalité mais une inclusion vu que l'ensemble des 3-1/n avec n entier n'est évidement pas égal à [2,3[. La démarche fonctionne tout de même vu qu'au lieu d'obtenir que A est égal à l'ensemble vide, tu devrait obtenir que A est inclu dans l'ensemble vide, mais au final, ça revient au même.
- Ensuite, plus grave, si A est vide, alors "sup(A), max(A),..." ne sont surement pas égaux à "le vide" pour la bonne et simple raison que ces trucs (Sup, Max, ...), lorsqu'ils existent, ce sont des réels et que "le vide", c'est pas du tout un réel. Donc la conclusion finale, c'est qu'aucun d'entre eux n'existe.
Il faut évidement faire la différence entre le fait qu'un "truc" n'existe pas et le fait que le truc en question est vide : il n'y a aucun doute concernant le fait que "le vide", ça existe (en tout cas en math).
A mon avis, c'est une erreur lié au fait qu'au Lycée, de façon mécanique et sans réfléchir, lorsque l'on demande à des élèves de résoudre une équation, ils terminent leur prose par S=... avec, comme toujours, aucune phrase d'explication sur ce que désigne S.
Si une équation, par exemple f(x)=0 n'a pas de solutions, ça signifie qu'il n'existe pas de x tel que f(x)=0, mais par contre, l'ensemble des solutions, c'est à dire l'ensemble des x vérifiant f(x)=0, lui il existe (et il est vide).
Pour prendre une analogie dans la vie courante, si un panier est vide, alors ce qui n'existe pas, c'est un objet qui soit à l'intérieur du panier. Par contre, le panier, bien que vide, lui il existe...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: (L2) exo d'ensembles (bornes sup,inf,minimum,maximum)
C'est un exo du partiel de l'année précédente, même le premier exo de l'énoncé, un "piège" d'entrée de jeu c'est mesquin en effet
Que je sois bien fixé sur la rédaction acceptée : (c'est vraiment pas mon point fort..)
ça donne donc :
A inclu dans [0,2] inter [2,3[ inter (R\Q)
=> A inclu dans {2\Q}
=> A inclu dans {le vide}
donc A est vide (ça se note A=le vide non?) Là j'ai peur de ne pas comprendre toute la subtilité de ce que tu expliques Ben
donc max A,min A, inf A, sup A n'existent pas car A est vide ?
Que je sois bien fixé sur la rédaction acceptée : (c'est vraiment pas mon point fort..)
ça donne donc :
A inclu dans [0,2] inter [2,3[ inter (R\Q)
=> A inclu dans {2\Q}
=> A inclu dans {le vide}
donc A est vide (ça se note A=le vide non?) Là j'ai peur de ne pas comprendre toute la subtilité de ce que tu expliques Ben
donc max A,min A, inf A, sup A n'existent pas car A est vide ?
Re: (L2) exo d'ensembles (bornes sup,inf,minimum,maximum)
Ce que je t'explique, ça semble pourtant pas bien compliqué : un panier vide, ça existe et donc la phrase "le panier est vide", n'a pas grand chose à voir avec l'affirmation "le panier n'existe pas" (*)
Dans le contexte de l'exo, ça signifie que ce que tu as écrit, à savoir que "sup(A)=le vide" est faux et que ça n'a rien à voir avec ce que tu aurais du écrire (et qui est vrai), à savoir "sup(A) n'existe pas".
Sinon au niveau de ton dernier post, sur l'idée, c'est O.K., mais la syntaxe, c'est n'importe quoi.
Le symbole / (="privé de") ce qu'on met avant et après, c'est des ensembles et, par exemple, 2\Q, ben ça veut rien dire vu que 2, c'est pas un ensemble (c'est un réel).
Si tu veut parler de l'ensemble dont l'unique élément est le réel 2, c'est {2} donc {2}\Q ça, ça a du sens (et c'est l'ensemble vide).
Et réciproquement, {x,y,z}, c'est l'ensemble dont les éléments sont x,y et z donc de rajouter des accolades en pus en écrivant {{2}\Q}, ça veut dire que tu parle de l'ensemble qui a pour unique élément {2}\Q, c'est à dire l'ensemble vide. Et comme cet ensemble {{2}\Q} contient effectivement un élément (à savoir l'ensemble vide), il n'est pas vide (c'est comme si tu mettait une petite boite d'allumette vide à l'intérieur d'une grosse boite d'allumette : la grosse boite n'est pas vide vu qu'elle contient la petite)
Dans le contexte de l'exo, ça signifie que ce que tu as écrit, à savoir que "sup(A)=le vide" est faux et que ça n'a rien à voir avec ce que tu aurais du écrire (et qui est vrai), à savoir "sup(A) n'existe pas".
Sinon au niveau de ton dernier post, sur l'idée, c'est O.K., mais la syntaxe, c'est n'importe quoi.
Le symbole / (="privé de") ce qu'on met avant et après, c'est des ensembles et, par exemple, 2\Q, ben ça veut rien dire vu que 2, c'est pas un ensemble (c'est un réel).
Si tu veut parler de l'ensemble dont l'unique élément est le réel 2, c'est {2} donc {2}\Q ça, ça a du sens (et c'est l'ensemble vide).
Et réciproquement, {x,y,z}, c'est l'ensemble dont les éléments sont x,y et z donc de rajouter des accolades en pus en écrivant {{2}\Q}, ça veut dire que tu parle de l'ensemble qui a pour unique élément {2}\Q, c'est à dire l'ensemble vide. Et comme cet ensemble {{2}\Q} contient effectivement un élément (à savoir l'ensemble vide), il n'est pas vide (c'est comme si tu mettait une petite boite d'allumette vide à l'intérieur d'une grosse boite d'allumette : la grosse boite n'est pas vide vu qu'elle contient la petite)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 23 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
