Exo defi : Equadiff

[Nightmare]

Salut a vous :happy3:

Quelles sont les fonctions derivables verifiant ?

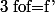
Quid si l'on prend holomorphe ? (Je n'ai pas encore de reponse a cette question, mais j'ai ma petite idee !)

Amusez-vous bien !

[Nightmare]

Apres reflexion devant mon brouillon, ma preuve pour le premier cas n'est pas complete non plus ... :mur:

[Nightmare]

Rapidement, pour ceux qui cherchent, j'ai trouvé pour le cas f réelle et croissante que seule la fonction nulle convenait. Je n'ai rien pour le cas décroissant pour le moment... Pour le cas complexe, je pense avec un contre exemple de la forme avec x et y deux complexes à préciser.

[Ben314]

Salut,
J'ai pas eu le temps de chercher grand chose, mais dans le cas réel, j'ai quand même vu ça :
S'il existe a0 sur ]a,b[ ; =0 sur [b,c] ; <0 sur ]c,d[ [ou le contraire] alors on a :
a) f est strictement croissante sur ]a,b[ et est >0 sur ]f(a),f(b)[
b) f est strictement décroissante sur ]c,d[ et est <0 sur ]f(d),f(c)[
Sauf que, vu que f(b)=f(c), c'est assez notoirement contradictoire...

[ffpower]

De mon coté, j ai obtenu la monotonie de f (cas réel)
Soit a tel que f'(a) est non nul, disons f'(a)>0. f étant C^1, f est strictement croissante au voisinage de a. Supposons maintenant qu'il existe b différent de a tel que f(b)=f(a), avec disons b>a. On choisit b minimal, de sorte que f>f(a) sur ]a,b[. Alors cette inégalité entraine que f '(b) est négatif, ce qui est absurde puisque f(a)=f(b) implique f '(a)=f '(b). Avec cette méthode on obtient ainsi que si f '(a) est non nul, alors la valeur f(a) n'est prise qu'en a. Il en découle aisément ( je crois^^ ) que f est monotone