Equadiff avec serie entiere

[Daewin]

quel produit ?

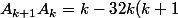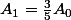
puis est-ce normal qu'avec cette formule je ne retrouve pas mes et ?

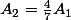
on n'utilise toujours pas les conditions initiales ?

:hein:

[Sa Majesté]

Salut

J'ai fait les calculs de mon côté et je ne trouve pas la même relation de récurrence
Je trouve pour
Et elle marche aussi pour k=0 et pour k=1
Je pense que ça vient de tes changements de variable

[girdav]

Vues les conditions initiales, je crois qu'il est préférable de chercher une solution de la forme .

[Daewin]

donc on a pour

comment à partir de ça, on arrive à trouver la solution y(x) ?
il y a une méthode générale ?

[Sa Majesté]

Eh bien comme l'a dit girdav tu peux trouver Ak en fonction de k (et de A0)

[Daewin]

oui mais je n'ai pas compris comment faire ...

[Sa Majesté]

Tu pars de pour k=1 à n
et tu multiplies ces égalités pour obtenir en fonction de n

[Daewin]

Tu pars de pour k=1 à n
et tu multiplies ces égalités pour obtenir en fonction de n

:marteau: je n'ai toujours pas compris ce qu'on multiplie ^^ désolé :triste:

et c'est ce que devrais trouver si je refais mes calculs du début ? moi c'était en plus

[Sa Majesté]

Petite question : tu fais quoi comme études ?

Sinon ben une fois que tu as la relation de récurrence , pour obtenir il suffit de changer k en k-1





...







Et puis tu multiplies toutes ces égalités
C'est qd même pas très très dur ... :zen:

[Daewin]

non effectivement ce n'était pas si dur ! je n'avais pas compris ça comme ça lol
c'est la méthode de développement en série entière avec laquelle j'ai du mal à voir les étapes successives pour avoir au final la solution de l'équation

sinon je suis en L2 physique, les maths c'est pas mon dada mais je persévère :)

[Daewin]

alors quelle serait l'étape suivante pour avoir la solution finale ?

[Daewin]

vous êtes partis en wk prolongé ? :zen: