Existence d'une intégrale

[flo22]

Bonjour,

je dois prouver l'existence d'une intégrale du type :



si je calcule cette intégrale et si que je montre que mon résultat admet des limites en , c'est suffisant ?

Merci

[sky-mars]

Hello

Tu dois tout d'abord :
1) Montrer que f est continue sur un segment [a,b]

donc existe
2) Tu regardes ce qu'il se passe au voisinage de
si par exemple c'est une fonction positive, tu cherche un équivalent de référence et à l'aide de critère comme celui de Riemann (par exemple), si c'est pas bon tu fais la règle du etc.. ou bien d'autre critère tout dépend de la fonction que tu as.
tu conclus sur l'intégrabilité
3) de même en -
4) tu conclus

[girdav]

Bonjour.
Si a une primitive simple, ça marche.
Sinon il faut faire ce qu'indique sky-mars.

[flo22]

alors ton point 2), je n'y comprends absolument rien ! équivalent de référence ? critère de Riemann ? règle du ?

[flo22]

Simple=calculable ?

[girdav]

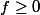
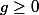
Equivalent: Si et et que
alors a la même nature que .
Règle du Si
alors converge.

[girdav]

Simple=calculable ?

Oui, par exemple dans le cas de on a une primitive et comme elle admet une limite en alors l'intégrale converge.
Mais ce n'est pas souvent le cas.
Quelle est ta fonction dans ton cas?

[flo22]

C'est du cours de sup ça ?
Je crois que je vais m'en tenir au calcul de l'intégrale, je dois le faire de toutes façons.

la fonction est :
dont une primitive est (en faisant gicler sgn(t) en décomposant l'intégrale)
Merci !

[xyz1975]

Bonjour,

je dois prouver l'existence d'une intégrale du type :



si je calcule cette intégrale et si que je montre que mon résultat admet des limites en , c'est suffisant ?

Merci

Oui, il suffit juste de justifier l'existence de ton intégrale, dire que f est continue je pense que c'est une condition très forte, ils en existent des classes plus larges de fonctions intégrables (monotones, continues par morceaux, bornées avec certaines conditions).

[flo22]

OK merci à tous :happy2: