" Existence " d'une intégrale sur un intervalle ?

[Wenneguen]

Bonjour,

quand on demande de montrer l'existence d'une intégrale sur un intervalle quelconque, doit-on montrer que l'intégrale est convergente, ou montrer que l'intégrande est intégrable sur l'intervalle en question ?

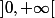
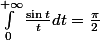
De plus, la distinction fonction intégrable sur un intervalle et intégrale convergente ne met-elle pas en évidence une " mauvaise " définition de l’intégrabilité ? ( en effet, n'est pas intégrable sur , et pourtant on a ... n'y a-t-il pas une certaine incohérence ? )

Merci :we:

[Nightmare]

Salut,

pour montrer l'existence d'une intégrale, on doit montrer sa convergence et il suffit de montrer qu'elle est intégrable (ce qui implique la convergence).

La différence entre fonction intégrable et intégrale convergente est la même que celle entre une série absolument convergente et une série simplement convergente. Pour l'une on a des théorèmes plus forts qui en découlent et que l'on perd si l'on ne demande plus à ce que la convergence soit en module.