Existence polynôme

[mehdi-128]

Bonjour, je vois pas comment traiter cette question :

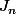
Montrer que, pour tout entier naturel N, il existe un polynôme unique tel que :



Merci.

[Sylviel]

La récurrence est un moyen...

[Dlzlogic]

Bonjour,
Avez-vous essayé avec les formules de multiplication des arcs ?
sin ma = ...
cos ma = ...
sin (n+1)a = ...
Si vous ne connaissez pas, je vous les donne.

[mehdi-128]

Bonjour,
Avez-vous essayé avec les formules de multiplication des arcs ?
sin ma = ...
cos ma = ...
sin (n+1)a = ...
Si vous ne connaissez pas, je vous les donne.

Non je connais pas ...

[Dlzlogic]

Convention [Cn;m] Combinaison de m objets n à n
sin ma = [C1;m]sin a cos^m-1 a - [C3;m]sin^3 a cos^m-3 a + [C5;m]sin^5 a s^^m-6 a - ...
cos ma =cos^m a - [C2;m]sin^2 a cos^m-2 a + [C4;m]sin^4 a cos^m-4 a ...
sin(m+1)a = 2 cos a sin ma - sin (m-1)a
cos(m+1)a = 2 cos a cos ma - cos(m-1)a

Si je ne me suis pas trompé. Mais rassurez-vous, c'est pas de mémoire.

[mehdi-128]

Convention [Cn;m] Combinaison de m objets n à n
sin ma = [C1;m]sin a cos^m-1 a - [C3;m]sin^3 a cos^m-3 a + [C5;m]sin^5 a s^^m-6 a - ...
cos ma =cos^m a - [C2;m]sin^2 a cos^m-2 a + [C4;m]sin^4 a cos^m-4 a ...
sin(m+1)a = 2 cos a sin ma - sin (m-1)a
cos(m+1)a = 2 cos a cos ma - cos(m-1)a

Si je ne me suis pas trompé. Mais rassurez-vous, c'est pas de mémoire.

J'ai rien compris : c'est illisible

Jamais entendu parlé des formules avec les combinaisons.

[Skullkid]

Si tu as essayé la récurrence, comme te l'a conseillé Sylviel, où bloques-tu ?

[GagaMaths]

mehdi tu as deja eu un pb avec des recurrences, je t'avais dit que , le plus souvent , quand tu dois d"montrer un truc "pour tout n" ou dans le genre, il faut tt de suite penser à une récurrence !

[mehdi-128]

J'ai fait ma récurrence mais je bloque à un moment :

Initialisation :

L'égalité est vérifiée en prenant

Hérédité : on suppose que la propriété est vraie au rang n. Montrons qu'elle l'est au rang n+1.





D'après l'hypothèse de récurrence :



Mais là je vois plus quoi faire :mur:

[Skullkid]

Ok, comme tu peux le constater, le premier terme de ta somme est sous la forme voulue, donc il faut t'occuper du deuxième terme. Le 2^n n'étant qu'un facteur indépendant de théta, tu pourras toujours le faire apparaître de force, donc ce qu'il faut pour commencer, c'est faire apparaître un sin(théta) dans le deuxième terme.

[mehdi-128]

Ok, comme tu peux le constater, le premier terme de ta somme est sous la forme voulue, donc il faut t'occuper du deuxième terme. Le 2^n n'étant qu'un facteur indépendant de théta, tu pourras toujours le faire apparaître de force, donc ce qu'il faut pour commencer, c'est faire apparaître un sin(théta) dans le deuxième terme.

Or :



En factorisant :




C'est correct ?

[Skullkid]

C'est correct (juste, pour faire apparaître exactement la forme voulue, il faut un 2^(n+1) en facteur au début, mais bon tu pourras toujours refactoriser après).

Donc, ce qu'il te reste à faire c'est de transformer , là y a plusieurs façons de faire.

[mehdi-128]

C'est correct (juste, pour faire apparaître exactement la forme voulue, il faut un 2^(n+1) en facteur au début, mais bon tu pourras toujours refactoriser après).

Donc, ce qu'il te reste à faire c'est de transformer , là y a plusieurs façons de faire.

Je pense qu'on peut dire que :






C'est bon ?

[Skullkid]

Oui, et il ne te reste plus qu'à prouver que c'est un polynôme en cos(2theta), ce qui n'est pas très dur si tu as déjà vu les polynômes de Tchebychev. Sinon, il va falloir que tu montres par récurrence que cos(nx) est un polynôme en cos(x).

[mehdi-128]

Oui, et il ne te reste plus qu'à prouver que c'est un polynôme en cos(2theta), ce qui n'est pas très dur si tu as déjà vu les polynômes de Tchebychev. Sinon, il va falloir que tu montres par récurrence que cos(nx) est un polynôme en cos(x).

En gros, faut que je montre que :



est un polynôme en

J'écris :



Donc :



Après je vois pas trop.

Ni la relation entre et

[Skullkid]

Tu vas pas y arriver sans faire une autre récurrence. Démontre, à côté, un résultat assez connu (je pensais que tu l'aurais déjà vu) : pour tout entier n, il existe un polynôme Tn tel quel que pour tout x réel, cos(nx) = Tn(cos x).

[mehdi-128]

Tu vas pas y arriver sans faire une autre récurrence. Démontre, à côté, un résultat assez connu (je pensais que tu l'aurais déjà vu) : pour tout entier n, il existe un polynôme Tn tel quel que pour tout x réel, cos(nx) = Tn(cos x).

J'ai vu la démo sur le net du théorème suivant :

Soit n un entier naturel. Il existe un et un seul polynôme noté Tn tel que
R,

Mais bon j'aurais mon en fonction de alors que dans la récurrence il me faut en fonction de non ? Y a pas un souci ?

Sinon, avez-vous une idée de comment démontrer l'unicité du polynômeJn ?

[Skullkid]

Tu as un résultat, indépendamment de ton exercice : il existe un unique polynôme tel que cos(nx) = Tn(cos x). Dans ton exo à toi, tu en es arrivé à des machins du genre cos(2n theta) donc c'est bon, tu peux prendre x = 2theta. L'unicité viendra du fait que tu auras une relation de récurrence entre Jn et J(n+1).

[mehdi-128]

Tu as un résultat, indépendamment de ton exercice : il existe un unique polynôme tel que cos(nx) = Tn(cos x). Dans ton exo à toi, tu en es arrivé à des machins du genre cos(2n theta) donc c'est bon, tu peux prendre x = 2theta. L'unicité viendra du fait que tu auras une relation de récurrence entre Jn et J(n+1).

Ah merci :we:

En quoi une relation de récurrence entre Jn et J(n+1) assure l'unicité ?

Je suppose que pour démontrer l'unicité il faut partir de Jn et Jn' et montrer qu'ils sont égaux.

[Sylviel]

Tu ne peux construire qu'un seul Jn+1 à partir de Jn...

Pour le degré du polynome cela provient aussi de ta relation de récurrence.