Exercie pour le fun
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Anonyme
 par Anonyme » 13 Jan 2009, 21:05
par Anonyme » 13 Jan 2009, 21:05
Salut !
Je suis en sup. Nous avons terminé le chapitre de continuité et nous sommes en plein chapitre de dérivation. C'est là que se pose une question (en fait c'est plutôt un problème) assez résistante.
Soit
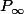
= {
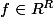
,
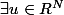
,
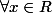
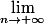
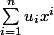
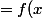)
}
soit
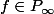
et u tel que : ,
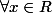
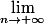
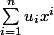
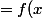)
u est-elle l'unique suite vérifiant cette propriété ?
f est elle continue, dérivable sur R ?
on note diff(f) (sous reserve d'exitence)
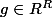
,
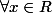
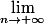
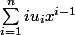
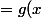)
si f est dérivable a t-on f ' = g ?
Voilà merci d'avance !!!
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 13 Jan 2009, 21:41
par Doraki » 13 Jan 2009, 21:41
Oui, tout est vrai.
Le truc important c'est de montrer que si u est une suite pour laquelle f est bien définie sur R tout entier,
alors pour tout x de R, la suite (un * x^n) tend vers 0,
et que pour tout x de R, la série de terme général |un|x^n est convergente
Une fois qu'on sait ça on peut manipuler ces séries beaucoup plus facilement et montrer que f est continue, dérivable, que f' = diff(f), que la suite u est unique, que f est indéfiniment dérivable... etc
-
Anonyme
 par Anonyme » 15 Jan 2009, 18:05
par Anonyme » 15 Jan 2009, 18:05
Salut !
Merci pour le coup de pouce ( et désolé de te répondre si tard). Je n'avait pas pensé à la convergence de la série de terme général |un|x^n . Je pense pouvoir m'en sortir avec cette indication.
Merci encore pour ton aide.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 77 invités
