Bonjour, je suis en deuxième année de prépa et je bloque sur un exercice pourriez vous m'aider s'il vous plaît ? Voici l'énoncé de l'exercice :E un R espace vectoriel de dimension finie n >2. Soit p et q deux projecteurs non triviaux, tel que p+q≠ IdE et poq=qop
Montrer que Sp (p+q) est inclus dans {0,1,2} puis établir une relation entre Im p et Im q équivalente à (2 appartient à Sp (p+q))
Exercice valeurs propres
3 messages
- Page 1 sur 1
Re: Exercice valeurs propres
par Ben314 » 03 Jan 2019, 23:06
Salut,
(1) Montre que)
est un sous espace stable de 
ce qui permet de considérer la restriction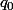 
de à . Vérifie alors que 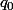est un projecteur et déduit en que \!=\!\ker(q_0)\!\oplus\!\text{im}(q_0))
.
(2) Montre que)
est un sous espace stable de ce qui permet de considérer la restriction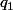 
de à . Vérifie alors que 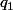est un projecteur et déduit en que \!=\!\ker(q_1)\!\oplus\!\text{im}(q_1))
.
(3) Tu as alors\!\oplus\!\text{im}(p)=\ker(q_0)\!\oplus\!\text{im}(q_0)\!\oplus\!\ker(q_1)\!\oplus\!\text{im}(q_1))
.
Si un vecteur se décompose sous la forme
dans cette décomosition de 
, que vaut )
? que vaut )
? que vaut (x))
?
(1) Montre que
(2) Montre que
(3) Tu as alors
Si un vecteur se décompose sous la forme
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Exercice valeurs propres
par Aidemaths1 » 03 Jan 2019, 23:55
x1 x2 appartiennent à Ker p donc p(x) = p(x3) +p(x4)
Et q(x)= x2 + x3
donc (p+q)(x)=p(x3) + p(x4) + x2 + x3
Et q(x)= x2 + x3
donc (p+q)(x)=p(x3) + p(x4) + x2 + x3
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 44 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :